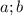Впрямоугольном треугольнике авс гипотенуза ав =10см,а катет ас =5см . найти второй катет и острые углы треугольника

👇

Ответ:

mikhailkoltsov

25.02.2023

Так как есть гипотенуза, то треугольник ABC- прямоугольный
BC выражаем через теорему Пифагора:
с²=а²+b²
a²=c²-b²
a=√(c²-b²) (скобки обозначают, что находится под корнем)
BC=√(10²-5²)=√(100-25)=√75=√(25*3)=5√3
Острые углы находим через синусы ( можно через косинусы)
sinB=AC/AB=5/10=1/2.
Как мы заем, sin30°=1/2
∠A=180°-(90°+30°)=60°
ответ: BC=5√3, ∠A=60°, ∠B=30°

4,4(87 оценок)

Открыть все ответы

Ответ:

Мариелла17

25.02.2023

Обозначим стороны как a;b

. И пусть

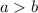тогда большая высота опускается на меньшую сторону , меньшая на большую . Тогда площадь с одной стороны равна S=3b

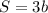, с другой стороны S=2a

.
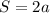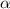Вспомним что угол между высотами проведенные с тупого угла равен острому углу параллелограмма.Учитывая это обозначим угол между высотами как $\alpha$ тогда острый угол равен 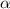$\alpha$ следовательно тупой 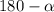$180- \alpha$ . Из прямоугольных треугольников которые образовались после проведения высота соответственно на стороны a ;b

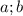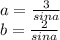равны $a=\frac{3}{sina}\\
b=\frac{2}{sina}$ тогда площадь запишится как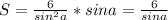
$S=\frac{6}{sin^2a}*sina=\frac{6}{sina}$
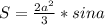но и она же равна $S=\frac{2a^2}{3}*sina$ приравняем
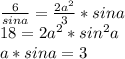$\frac{6}{sina}=\frac{2a^2}{3}*sina\\
18=2a^2*sin^2a\\
a*sina=3$ -3 нам не подходит потому что синус в I;II

четверти положителен
Диагональ выразим по теореме косинусов
$5^2=a^2+\frac{4a^2}{9}-2*a*\frac{2a}{3}*cos(180-a) \\
5^2=a^2+\frac{4a^2}{9}+\frac{4a^2}{3}*cosa\\
cosa=\frac{25-a^2-\frac{4a^2}{9}}{\frac{4a^2}{3}}\\
$
с первого равенство выразим синус через косинус затем подставим и решим уравнение перейдем в общем к такому
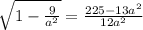$\sqrt{1-\frac{9}{a^2}}=\frac{225-13a^2}{12a^2}\\
$ решая это уравнение получим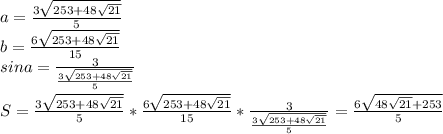
$
a=\frac{3\sqrt{253+48\sqrt{21}}}{5}\\
b=\frac{6\sqrt{253+48\sqrt{21}}}{15}\\
sina=\frac{3}{\frac{3\sqrt{253+48\sqrt{21}}}{5}}\\\\
S=\frac{3\sqrt{253+48\sqrt{21}}}{5}*\frac{6\sqrt{253+48\sqrt{21}}}{15}*\frac{3}{\frac{3\sqrt{253+48\sqrt{21}}}{5}}=\frac{6\sqrt{48\sqrt{21}+253}}{5}$
оно примерно равна 26

Найти площадь параллелограмма. если его наибольшая диагональ равна 5 см. а две его высоты, соответст

4,6(13 оценок)

Ответ:

salihvalishev

25.02.2023

Диагональ с двумя высотами образует 2 треугольника.
Обозначим углы против этих высот за α и β.
Тогда sin α = 3/5. а sin β = 2/5.
cos α = √(1-9/25) = 4/5
cos β = √(1-4/25) =√21/5.
Острый угол параллелограмма равен сумме α и β.
Для определения площади параллелограмма надо найти его основание, которое равно 5*cos α - 3 / tg(α+β).
tg(α+β) = (tg α+tg β) / (1 - tg α*tg β).
tg α = sin α / (1-sin²α) = (3/5) / (√(1-9/25)) = 3 / 4,
tg β = (2/5) / (√(1-4/25)) = 2 / √21.
tg(α+β) = ((3/4)+(2/√21)) / (1-(3/4)+(2/√21)) = 1,76376.
Основание равно 5*(4/5) - 3/1,76376 = 2,29909.
Площадь параллелограмма равна: 3*2,29909 = 6,89727.

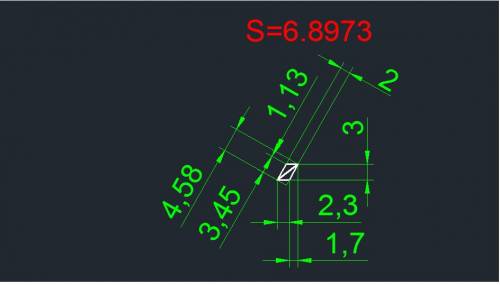
Найдите площадь параллелограмма, если его большая диагональ равна 5, а высоты равны 2 и 3.