В треугольнике ABC ∠C = 120°, CK—биссектриса.
Доказать, что 1 / CK = 1 / AC+1 / BC. || 1 / lc = 1 / a + 1 / b ||
- - - - - - - - - - - - - - - - - - - - - - - - - - -
CK = 2*AC*BC*cos(∠ACB /2) / (AC+BC)
CK= 2*AC*BC*cos(120°/2) / (AC + BC) || cos60° =1 /2 ||
CK= AC*BC / (AC+BC) ⇔ 1 / CK = (AC+BC) / AC*BC
1 / CK = AC / AC*BC + BC / AC*BC
1 / CK = 1 / AC+ 1 / BC ч. т. д.
= = = = = = = = = = = = = = = = = = = = = = = = = = = = =
* * * P.S. ∠ACB = ∠C ; ACK =∠BCK =∠ ACB /2 = ∠C /2
CK = Lc = 2abcos(∠C/2) / (a+b) * * *
действительно :
S(ΔACB) =S(ΔACK) + S(ΔBCK) ;
(1/2)*AC*BC*sin∠C=(1/2)*AC*CK*sin(∠C/2) + (1/2)*BC*CK*sin∠C/2)
(1/2)*AC*BC*sin∠C =(1/2)*CK*sin(∠C/2) *(AC + BC)
* * * ! sin2α = 2sinα*cosα * * *
* * * sin∠C = sin(2*∠C/2) = 2sin(∠C/2)*cos(∠C/2) * * *
2AC*BC*cos(∠C/2) = CK* (AC + BC) ;
CK =2AC*BC*cos(∠C/2) / (AC+BC) || Lc=2abcos(∠C/2)/(a+b) ||
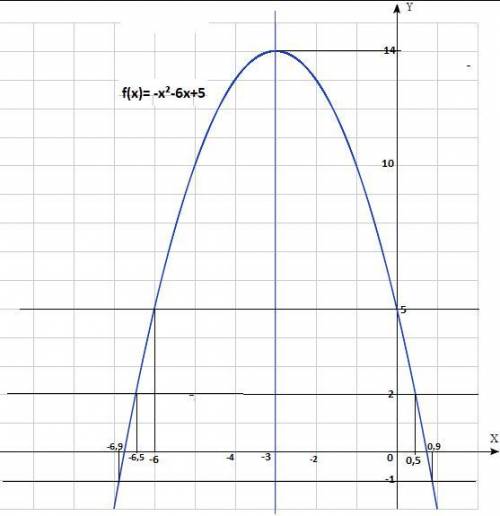
Постройте график функции f(x)= -x²-6x+5
Объяснение:
Это парабола ,ветви вниз . Координаты вершины
х₀=-в/2а, х₀=-(-6)/(-2)= -3 , у₀=-(-3)²-6*(-3) +5= 14 , ( -3; 14).
Доп.точки f(x)= -x²-6x+5:
х: -6 -5 -4 -2
у: 5 10 13 13.
1) f(x)=5 при х=0 , х=-6.
5= -x²-6x+5, -x²-6x=0 , x²+6x=0 , х(х+6)=0 , х=0 , х=-6.
f(x)=2 при x≈ 0,5 , x≈-6,5
2= -x²-6x+5, -x²-6x+3=0 , x²+6x-3=0 , D=48 ,x≈ 0,5 , x≈-6,5.
f(x)=-1 при x≈ 0,9 , x≈-6,9
-1= -x²-6x+5, -x²-6x+6=0 , x²+6x-6=0 , D=60 ,x≈ 0,9 , x≈-6,9 .
2) Нули функции f(x)=0 :
0= -x²-6x+5, x²+6x-5=0 , D=56 ,x=-3+√14 ≈0,74 , x=-3-√14 ≈-6,74 ,
Промежутки знакопостоянства функции :
f(x)>0 при -3-√14 <х< -3+√14 ;
f(x)<0 при х < -3-√14 и x>-3+ √14
3) Координаты вершины ( -3; 14). Ось симметрии х=-3
4) Наибольшее значение : f(x)=14.