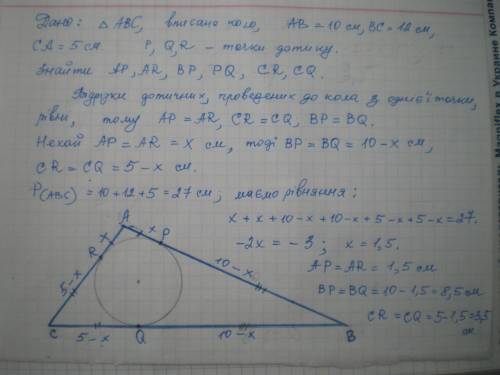
АР=1,5 см, РВ=8,5 см, BQ=8,5 см, QC=3,5 см, CR=3,5 см, RA=1,5 см.
Объяснение:
Первый признак равенства треугольников : по двум равным сторонам и равному углу между ними. В условии равные углы не образованы равными сторонами. Утверждать, что треугольники равны, нельзя (рис.1).
2. ∠BAC — прямой: ∠BAC = ∠EDF = 90°; (рис.2)
AB=DE (равные катеты); BC=EF (равные гипотенузы) ⇒
ΔABC = ΔDEF по равным катету и гипотенузе.
3. ∠BAC — тупой : ∠BAC = ∠EDF > 90°; (рис.3)
Так как в треугольнике может быть только один тупой угол, а два других будут острыми, то по теореме синусов
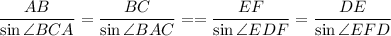
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD (оба острые)
⇒ ∠ABC = ∠DEF (по сумме углов треугольника) ⇒
ΔABC = ΔDEF по двум равным сторонам и углу между ними.
5. ∠BCA — прямой : Так как в треугольнике может быть только один прямой угол, а два других будут острыми, то по теореме синусов
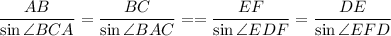
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD = 90°
ΔABC = ΔDEF по равным катету и гипотенузе.
=====================================
Остальные дополнительные условия недостаточны - видно на рисунках.
1. ∠BAC — острый - рис.1
4. ∠BCA — острый - рис.1
6. ∠BCA — тупой - рис.4
7. AB>BC — рис.1, рис.4
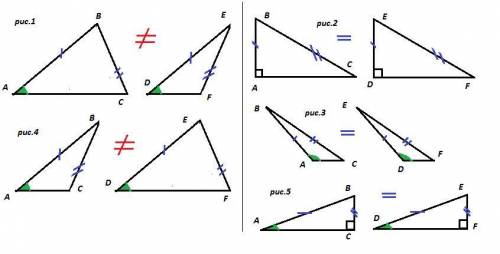
Рисунок приложен.
АР=AR (как касательные, проведенные с одной точки).Пусть они будут по у см
Аналогично BP=BQ=x,
CQ=CR=z
Составим 3 уравнения:
х+у=10
y+z=5
x+z=12
Z больше у на 2 (что можно понять)
y+y+2=5
2y=3
y=1,5
z=3,5
x=10-1,5=8,5
ответ: 1,5 см, 8,5 см, 8,5 см, 3,5 см, 3,5 см, 1,5 см