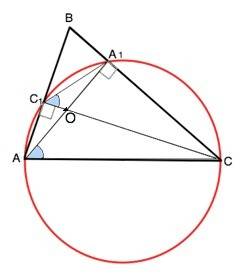
В ∆ АВС высоты АА1 и СС1 со сторонами два прямоугольных треугольника АС1С и АА1С с общей гипотенузой АС.
Следовательно, вокруг них можно описать окружность с диаметром АС, на который опираются прямые углы АС1С и АА1С.
Вписанные углы А1АС и А1С1С опираются на одну дугу А1С. Вписанные углы, опирающиеся на одну дуга, равны. ⇒
∠СС1А1=∠САА1. Доказано.---------
Рассмотрим ∆ АОС1 и А1ОС.
Эти треугольники подобны по двум углам - прямому при С1 и А1 и вертикальному при точке пересечения высот О.
Из подобия следует пропорциональность сторон:
С1О:А1О=АО:СО,
откуда имеем пропорциональность тех же сторон в ∆ АОС и ∆ А1ОС1.
Вертикальные углы при вершине О этих треугольников равны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следовательно, углы СС1А1 и САА1 равны. Доказано.
πRL=36π⇔RL =36⇒ L =36/R.
* * * L_длина образующей ,R_радиус основания * * *
V =(1/3)*πR²H =(1/3)*πR²√(L² -R²) =(1/3)*πR²√((36/R)² -R²)=
(1/3)*π√(36²R²-R⁴)=(1/3)*π√(1296R² - R⁴). * * * замена x =R² * * *
V=(π/3)√(1296x-x²) =(π/3)√(648²-(x²-2x*648+648²) )=(π/3)√(648²-(x-648)² ).
V=Vmax, если x =648⇒R² =648 ; R² =324*2 ; R =18√2 (см).
--- можно и с производной или применением неравенств---