Вступление:
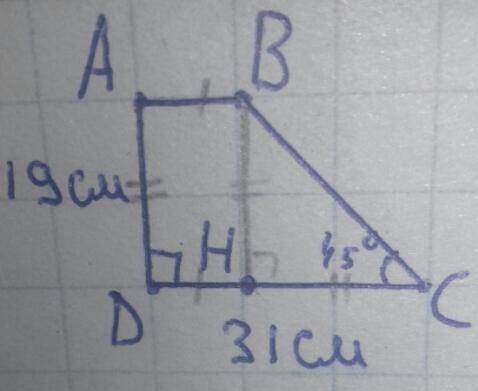
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
б) геометрич. место точек, удаленных от N на расст.2 см - окружность с центром в т.N и радиусом 2 см.
в) две точки пересечения этих двух окружностей (а и б) - одновременно удаленные.
г) если одновременно - это множ-во точек часть окружности с центром в т. М до точек пересечения с окружностью с центром в т.N и часть второй окружности с центром в т. N (как "откушеное яблоко").
е) существуют - 2 точки пересечения окружностей: первая с центром М и радиусом, напр., 3,5см, вторая с центром N и радиусом 1,5см.
ж) множество - это две точки пересечения окружностей, напр., радиусами по 3 см.