1 решение: угол А= углу В= 52°; угол С равен 76°
2 решение: угол А= углу В = 68°; угол С равен 44°
Объяснение:
решение 1
угол А и угол В равны ( по св-ву р/б треугольника следует, что углы, лежащие у его основания равны) => ни один из этих углов не может быть больше или меньше друг друга => угол С будет иметь разность с углами А и В, т. е. он может быть больше на 24° и меньше (получается, что задача имеет два решения, тк что угол А или В могут быть больше угла С, что он может быть больше угла А или В).по сумме углов трекгольника следует, что:180°-2x=x+24° (за х мы обозначили равные углы А и В, а 24° это то, насколько угол С больше углов А и В)180°-3х=24°х=(180°-24°):3 = 156°:3=52° х+24°=52°+24°=76° (это угол С в том решении, когда он больше А и В на 24°)
решение 2
180-2x=x-24
180-3x=-24
=>3x= 180°+24°=204°=>x=204°:3=68°(это у нас будут углы А и В, тк во втором решени они будут на 24° больше, чем С)
по сумме углов т-ка:
180-(68+68)=180-136=44°( это у нас С)
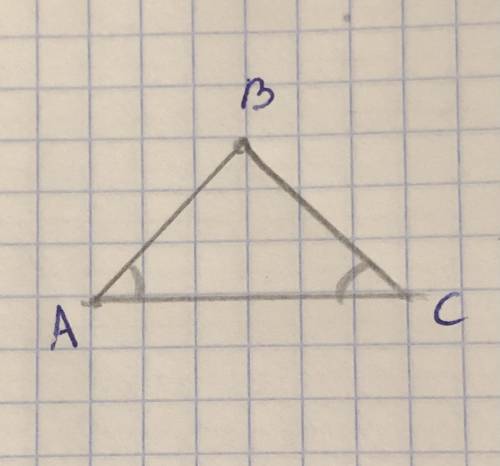
Дано: ΔABE - равнобедренный, АВ=ВЕ= 17 см, АЕ= 16 см, АЕВ∈α, CB⟂α, C∉α, СВ= 8 см.
Найти: расстояние от точки C до стороны треугольника AE
Решение.
1) Проведём высоту ВН в равнобедренном треугольнике АВЕ => BH⟂AE
Так как BH⟂AE и по условию ВС⟂α, по теореме о трёх перпендикулярах следует, что наклонная СН⟂АЕ. Наклонная СН и есть расстоянием от точки С до стороны АЕ ΔABE.
2) В треугольнике ЕСВ (∠ЕВС=90°, т.к. СВ⟂α) по т.Пифагора находим гипотенузу ЕС:
ЕС²= ЕВ²+ВС²;
ЕС²= 17²+8²;
ЕС²= 289+64;
ЕС²= 353
3) Поскольку ΔABE - равнобедренный, а ВН - высота, проведённая к основанию АС, то ВН также является и медианой ΔАВЕ => АН=НЕ= ½АЕ= 16 : 2 = 8 см.
4) В ΔCHE (∠CHE=90°) по т.Пифагора находим СН:
СН²= ЕС² – НЕ²;
СН²= 353–8²;
СН²= 353–64;
СН²= 289;
СН= 17 см (–17 быть не может)
Расстояние от точки C до стороны треугольника AE равно 17 см.
ответ: 17 см.
Объяснение:
Обозначим СК как х, а КВ то гда как х+5.
Есть теорема, о том, что высота равна среднему геометрическому проекций катетов на гипотенузу, иначе:
АК=
6=
Чтоб его решить, возведем обе части в квадрат(вообще, надо учитывать, при каких х²+5х больше нуля, но пока это неважно):
36=х²+5х
х²+5х-36
D=25+144=169 - два корня
х₁=4 х₂=-9 - не подходит по усл.
⇒СК=4, а КВ=4+5=9.
Тогда СВ=13
Найдем остальные стороны по теореме Пифагора, так как ΔКАВ и ΔСАК - прямоугольные(по опр. высоты):
АВ²=АК²+КВ²
АВ²=36+81
АВ=√117
СА²=СК²+АК²
СА²=16+36
СА=√52
СА=2√13
ответ: 2√13, √117, 13