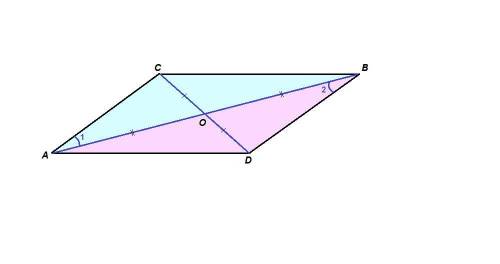
ответ: ∠АСВ = 112°
Объяснение:
1. АО = ОВ и CO = OD по условию,
∠АОС = ∠BOD как вертикальные, значит
ΔАОС = ΔBOD по двум сторонам и углу между ними.
Из равенства треугольников следует, что
АС = BD и ∠САО = ∠DBO.
2. Тогда в треугольниках АСВ и BDA:
АС = BD, ∠1 = ∠2, AB - общая сторона, значит
ΔАСВ = ΔBDA по двум сторонам и углу между ними.
3. ∠1 = ∠2, а эти углы - накрест лежащие при пересечении прямых АС и BD секущей АВ, значит
АС║BD.
∠АСВ + ∠CBD = 180°, так как эти углы соответственные при пересечении параллельных прямых АС и BD секущей ВС, тогда
∠АСВ = 180° - ∠CBD = 180° - 68° = 112°
В основании лежит правильный n-угольник, который делится отрезками от центра до вершин на n равнобедренных тр-ков. Угол при вершине тр-ка равен 360/n.Сумма углов одного тр-ка, примыкающих к основанию равна 180-(360/n) и она равна одному углу между сторонами n-угольника.
Сумма двугранных углов, прилежащих к боковым рёбрам n-угольной призмы равна удвоенному углу между сторонами n-угольника:
2*(180-(360/n))=360-(720/n) - ответ.