S=0.5*d^2*sin()=0.5*144*0.5=36 cм^2
Угол 125 градусов и угол 55 градусов называются односторонними и ВСЕГДА их сумма составляет 180 градусов
125+55=180 градусов
Если при пересечении двух прямых третьей секущей сумма односторонних углов равна 180 градусов,то прямые параллельны
Номер 2
Если внешние углы треугольника равны между собой,то равны и смежные им внутренние углы,а это обозначает,что треугольник равнобедренный,если одна из сторон равна 6 см,и это основание треугольника,а периметр равен 64 см,то каждая боковая сторона,а они в равнобедренном треугольнике равны между собой,равна
(64-6):2=29 сантиметров
Номер 3
Внешний и смежный ему внутренний угол в сумме равны 180 градусов
<А=180-120=60 градусов
Так как треугольник прямоугольный,то <В=180-(90+60)=30 градусов
Значит,АС+АВ=21 см ,где
АВ-гипотенуза
АС-катет,который расположен против угла 30 градусов
По определению,катет,лежащий против угла 30 градусов вдвое меньше гипотенузы
Катет-Х
Гипотенуза-2Х
Х+2Х=21
ЗХ=21
Х=21:3
Х=7
АС=7 см
АВ=7•2=14 см
Объяснение:
Объяснение:
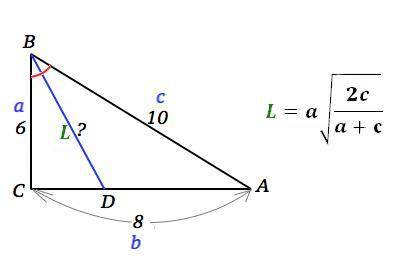
Отношение сторон данного треугольника 6:8:10=3:4:5 соответствует египетскому, т.е. прямоугольному.
а)
Биссектриса треугольника делит противоположную сторону на отрезки, соответственно пропорциональны двум другим сторонам. =>
СD:DА=ВС:ВА
СD:DА=6:10=3:5
АС=3+5=8 частей.
1 часть=8:8=1
СD=3•1=3
Из прямоугольного ∆ СВD по т.Пифагора ВD=√(ВС^2+СD^2)=√(36+9)=3√5
б)
Для биссектрисы острого угла прямоугольного треугольника есть формула
L=a•√(2c:(a+c)), где L- биссектриса, а и с -соответственно катет, прилежащий углу, и гипотенуза.
L=6•√(2•10:(6+10))=6√(5:4)=3√5
S=0.5*d^2*sin()=0.5*144*0.5=36 cм^2