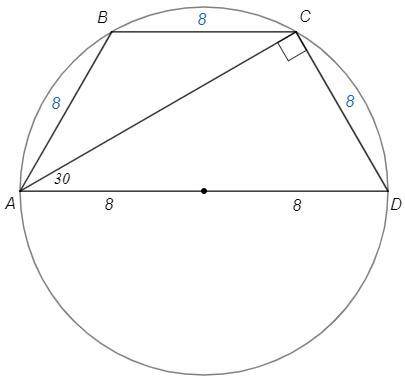
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)
Пусть треугольник абц, медиана проведена к стороне а, тогда ц=(22-а-б)/2, пусть м- длина медианы
составим систему уравнений
а-б=16-12
(22-а-б)/2+а+м=16
(22-а-б)/2+б+м=12
Если сложить 2 последних уравнения, то получится
22-а-б+а+м+б+м=28 -> 2м=6, отсюда м=3
Вот так