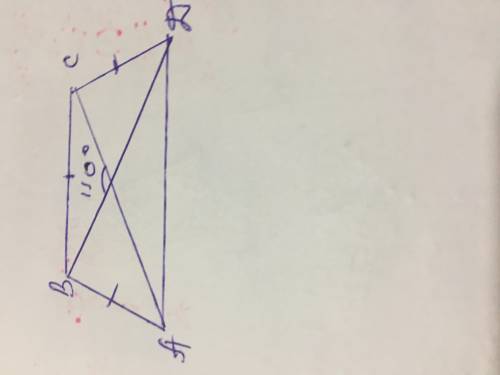
ответ:Диагонали равнобедренную трапецию делят на 4 треугольника,два треугольника,у которых одной стороной являются бОльшее или меньшее основание,равнобедренные,а два других,у которых в наличии боковые стороны трапеции,равны между собой
<ВОС=<АОD=110 градусов,как вертикальные
<ОВС=<ВСО=(180-110):2=35 градусов,как углы при основании равнобедренного треугольника ВСО
Треугольник АОD тоже равнобедренный
<ОАD=<ODA=(180-110):2=35 градусов
<АОВ=<СОD=(360-110•2):2=(360-220):2=140:2=70 градусов
В условии указано,что
ВС=АВ=СD
Рассмотрим треугольник АВС,он равнобедренный,т к
АВ=ВС по условию задачи
Следовательно,
<ВАС=<ВСА=35 градусов
Тогда,
<В=(180-35•2)=110 градусов
<С=<В=110 градусов,как углы при основании равнобедренной трапеции
<А=180-110=70 градусов,т к сумма углов прилежащих к боковой стороне равна 180 градусов
<D=<A=70 градусов,т к углы при основании равнобедренной трапеции равны между собой
Как было сказано выше-
Треугольник АВО равен треугольнику СOD по определению,значит
<АВО=<DCO=180-(70+35)=180-105=75 градусов
Объяснение:
Пусть угол 1 = 140 ⁰. Угол 1 = углу 4=140⁰, как ветикальные. Угол 1 + угол 2 = 180⁰(смежные)⇒угол 2=180⁰-140⁰=40⁰. Угол 2 = углу 3=40⁰, как вертикальные.
Угол 1 = углу 6=140⁰, как накрест лежащие при a//b, и секущей с. Угол 2 = углу 5=40⁰, как накрест лежащие при a//b, и секущей с. Угол 6=углу 8=140⁰, как вертикальные. Угол 5 = углу 7=40⁰, как вертикальные.
ответ: Углы 1, 4, 6, 8 = 140⁰. Углы 3, 2, 5, 7 = 40⁰