Объяснение:
Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.
2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК.
3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.
4. В трапеции ABCD: AB = BC = CD, CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС, проходит через середину BD.
5. Пусть AA1 и BB1 – высоты неравнобедренного остроугольного треугольника АВС, М – середина АВ. Окружности, описанные около треугольников AMA1 и BMB1 пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К, М и L лежат на одной прямой.
6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.
10–11 класс
1. AD и BE – высоты треугольника АВС. Оказалось, что точка C', симметричная вершине С относительно середины отрезка DE, лежит на стороне AB. Докажите, что АВ – касательная к окружности, описанной около треугольника DEC'.
2. Прямая а пересекает плоскость α. Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α?
3. Дана неравнобокая трапеция ABCD (AB||CD). Произвольная окружность, проходящая через точки А и В, пересекает боковые стороны трапеции в точках P и Q, а диагонали – в точках M и N. Докажите, что прямые PQ, MN и CD пересекаются в одной точке.
4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.
5. В выпуклом четырехугольнике ABCD: AC ⊥ BD, ∠BCA = 10°, ∠BDA = 20°, ∠BAC = 40°. Найдите ∠BDC. (ответ выразите в градусах.)
6. Пусть AA1, BB1 и CC1 – высоты неравнобедренного остроугольного треугольника АВС; окружности, описанные около треугольников АВС и A1B1C, вторично пересекаются в точке Р, Z – точка пересечения касательных к описанной окружности треугольника АВС, проведённых в точках А и В. Докажите, что прямые АР, ВС и ZC1 пересекаются в одной точке.
АС=6см
АВ=10см
ВС=8см
Объяснение:
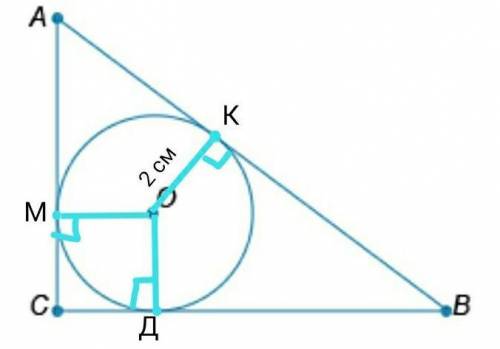
ДАНО: ∆АВС – прямоугольный, ∠С=90°; вписанная окружность с центром в точке О; К – точка касания; радиус=2см; ВК–АК=2см
НАЙТИ: АВ; АС; ВС
Стороны треугольника являются касательными к вписанной окружности. Обозначим точки касания Д и М, соединим О и М, О и Д. ОК, ОД и ОМ – радиусы. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, поэтому ОК⏊АВ, ОМ ⏊ АС и ОД ⏊ ВС. Получим четырехугольник МОДС. У него МО=ОД=2см. Если две прямые перпендикулярны третьей прямой, значит эти две прямые параллельны и так как ОМ и СД перпендикулярны АС, то ОМ || СД, и МС ⏊ ВС и ОД ⏊ ВС, значит
МС || ОД, а у четырехугольника, у которого противоположные стороны параллельны, они равны, поэтому ОМ=СД=2см, ОД=МС=2см → МОДС – квадрат. Пусть АК=х, тогда ВК=х+2. Отрезки касательных, соединяясь в одной точке равны от вершины до точки касания, поэтому:
АМ=АК=х, ВК=ВД=х+2, СМ=СД=2см. Тогда:
АС=2+х, АВ=х+х+2=2х+2, ВС=2+х+2=х+4
АС=2+х
АВ=2х+2
ВС=х+4
Составим уравнение, используя теорему Пифагора:
АС²+ВС²=АВ²
(2х+2)²=(2+х)²+(х+4)²
4х²+8х+4=4+4х+х²+х²+8х+16
4х²+8х+4=2х²+12х+20
4х²+8х–2х²–12х–20+4=0
2х²–4х–16=0
a=2, b= –4; c= –16
Д=b²–4ac=(–4)²–4•2•(–16)=16+128=144=12²
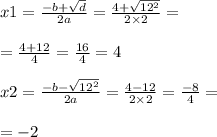
х₂= –2 нам не подходит, так как сторона не может быть отрицательной, тогда подходит х₁=4
АС=2+х=2+4=6см
АВ=2х+2=2•4+2=8+2=10см
ВС=х+4=4+4=8см
значит градусная мера дуги МN=40гр