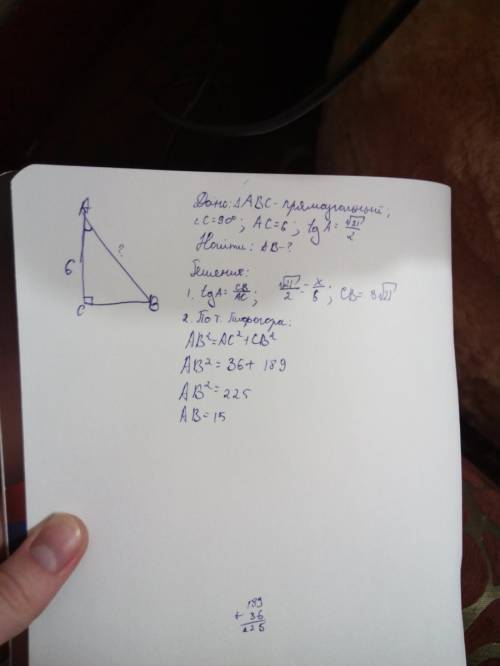
Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
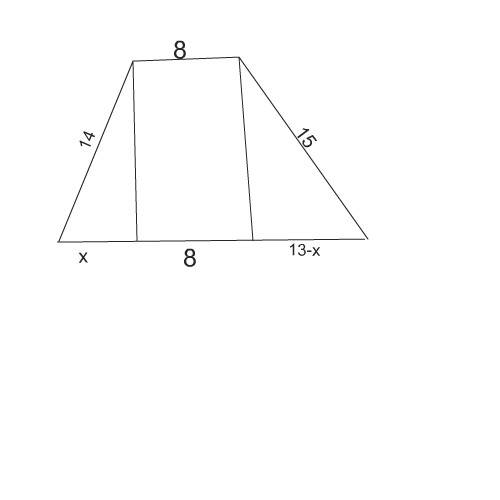
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
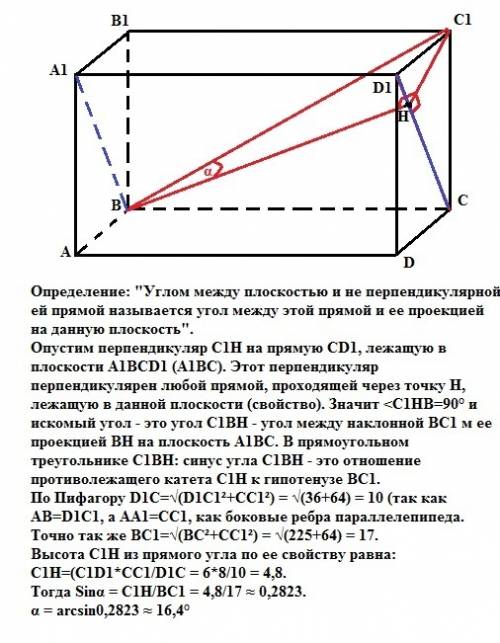
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.