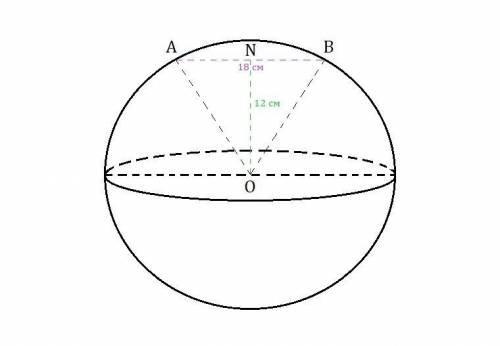
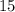см.
Проведём отрезк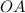и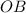 
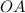и 
.
=======================================================
и 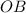- радиусы данной сферы ⇒ они равны.
⇒ 
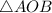- равнобедренный, где 
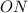- расстояние от точки 
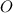до прямой 
и высота равнобедренного
Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является биссектрисой и медианой.
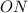⇒ - высота, медиана и биссектриса.
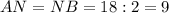см, так как 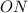- медиана.
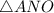- прямоугольный, так как 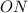- высота.
Найдём радиус 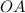по теореме Пифагора 
.
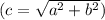см.
Итак, радиус данной сферы = 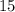см.
1) вектор AD (-6 - (-3); -3 - 5; 0 - (-6) ) = (-3; -8; 6)
координаты вектора находятся как разность координат конца и начала вектора
2) Расстояние между точками B и D это длина вектора BD
Вектор BD( -6 - 5; -3 - (-2); 0 - 4) = (-11; -1; -4)
Длина вектора это квадратный корень из суммы квадратов координат вектора т.е. \sqrt{ (-11)^{2} + (-1)^{2} + (-4)^{2} }
(−11)
2
+(−1)
2
+(−4)
2
= \sqrt{138}
138
3) Координаты середины отрезка это полусумма координат концов отрезка. Т.е.
точка М ( (-3+5)/2; (5 + (-2))/2 ; (-6+4)/2 ) = (1; 1,5; -1)
4) Произведение векторов AB и CD это сумма произведений их координат.
Сначала найдем вектора.
AB (5-(-3); -2-5; 4-(-6)) = (8;-7; 10)
CD (-6-0; -3-4; 0-3) = (-6; -7; -3)
Теперь перемножим координаты векторов и сложим их
AB * CD = 8*(-6) + (-7)*(-7) + 10*(-3) = -48+49-30 = -29
5) Угол между векторами можно найти из формулы векторного произведения векторов, которое равно произведению модулей векторов на косинус угла между ними.
Как уже было найдено в п4
AB (8;-7; 10) , CD (-6; -7; -3) и AB * CD = -29
Модуль |AB| равен \sqrt{ 8^{2} + (-7)^{2} + 10^{2} } = \sqrt{213}
8
2
+(−7)
2
+10
2
=
213
Модуль |CD| равен \sqrt{ (-6)^{2} + (-7)^{2} + (-3)^{2} } = \sqrt{ 94 }
(−6)
2
+(−7)
2
+(−3)
2
=
94
Тогда cos( \alpha ) =cos(α)= AB * CD / |AB| * |CD| = \frac{-29}{ \sqrt{213} * \sqrt{94} }
213
∗
94
−29
что приблизительно равно -0,204948276
6) Аналогично пункту 5
Угол между векторами можно найти из формулы векторного произведения векторов, которое равно произведению модулей векторов на косинус угла между ними.
Как уже было найдено ранее
вектор AD (-3; -8; 6)
Найдем вектор ВС
Вектор ВС (0-5; 4-(-2); 3-4) = (-5; 6; -1)
Теперь найдем AD * ВС = (-3)*(-5) + (-8)*6 + 6*(-1) = -39
Модуль |AD| равен \sqrt{ (-3)^{2} + (-8)^{2} + 6^{2} } = \sqrt{109}
(−3)
2
+(−8)
2
+6
2
=
109
Модуль |ВС| равен \sqrt{ (-5)^{2} + 6^{2} + (-1)^{2} } = \sqrt{ 62 }
(−5)
2
+6
2
+(−1)
2
=
62
Тогда cos( \alpha ) =cos(α)= AD * ВС / |AD| * |ВС| = \frac{-29}{ \sqrt{109} * \sqrt{62} }
109
∗
62
−29
что приблизительно равно -0,352767774
7) Вектор BD уже был найден BD(-11; -1; -4)
Вектор CB= - ВС = (5; -6; 1)
Найдем вектор AC (0-(-3); 4-5; 3-(-6) ) = (3; -1; 9)
Найдем сумму векторов AC и BD
AC(3; -1; 9) + BD(-11; -1; -4) = (3 + (-11); -1 + (-1); 9 + (-4) ) = (-8; -2; 5)
Теперь найдем произведение этого вектора на CB(5; -6; 1)
Произведение векторов равно (-8; -2; 5) * (5; -6; 1) = (-8)*5 + (-2)*(-6) + 5*1 = -23
8) Условие коллинеарности это пропроциональность координат векторов (если они не равны нулю)
В нашем случае AB(8;-7; 10) и CD(-6; -7; -3) не имеют нулевых координат, значит можно проверить на пропорциональность.
Очевидно
\frac{8}{-6} \neq \frac{-7}{-7} \neq \frac{10}{-3}
−6
8
=
−7
−7
=
−3
10
Следовательно вектора не коллинеарны.
