В треугольнике FCA FA=FC, AC=6 см, по теореме Пифагора FA=FC=3 корень с 2. В треугольнике АВС проведи высоту ВО. АО=ОС=3 см, угол А=углу С=30 градусов, сторона против угла 30 градусов в 2 раза меньше гипотенузы, то есть 2ВО=АВ. АВ2=ВО2+АО2, АВ2=0,25АВ2+АО2, 0,75АВ2=9, АВ=2 корень с 3. FB2=FA2-AB2=18-12=6, FB= корень с 6
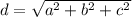. Измерения равны a,a,2a, тогда 
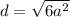, тогда измерения равны 2,2,4. Рассмотрим прямоугольный треугольник, в нем одна сторона - диагональ, другая - диагональ квадрата основания, третья - боковое ребро, тогда его стороны равны 2\sqrt{6
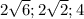}. Синус угла равен отношению бокового ребра к диагонали, то есть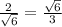
Чтобы найти синус угла между диагональю параллелепипеда и плоскостью основания, нужно рассмотреть прямоугольный треугольник, в котором этот угол находится, чтобы потом его оттуда найти. В данном случае стоит рассмотреть прямоугольный треугольник, в котором одна сторона - диагональ основания, другая - диагональ параллелепипеда, а третья - боковое ребро. В нем как раз будет нужный нам угол.
Треугольник АFС:
АС² = 2АF²
AF=√(АС²/2)=√18=3√2
Треугольник АВС:
АВ/sinC=BC/sinA=AC/sinB
AB=BC=AC*sin30/sin120=2√3
ТРеугольник ABF:
AF²=AB²+BF²
BF²=18-12=6
BF=√6 см