Сечение - правильный шестиугольник.
Объяснение:
Плоскости пересекаются по прямым линиям. Две параллельные плоскости пересекаются третьей по параллельным прямым.
Нам даны три точки секущей плоскости, пересекающей куб: E, F и G, расположенные на ребрах АВ, AD и DD1 соответственно.
Прямая EF, принадлежащая секущей плоскости и грани АВСD куба пересекает грань куба DD1C1C в точке Q, а грань куба AA1B1B в точке R.
Проведя прямую QG до пересечения с ребром D1C1, получим точку сечения Н.
Теперь можно провести НI параллельно EF и IK параллельно GF => получим все точки сечения.
Но можно построить недостающие точки P и S (построение понятно из рисунка) и провести прямые SI (через Н) и РК (через Е). Получим то же самое сечение, которое в силу симметричности точек является правильным шестиугольником.
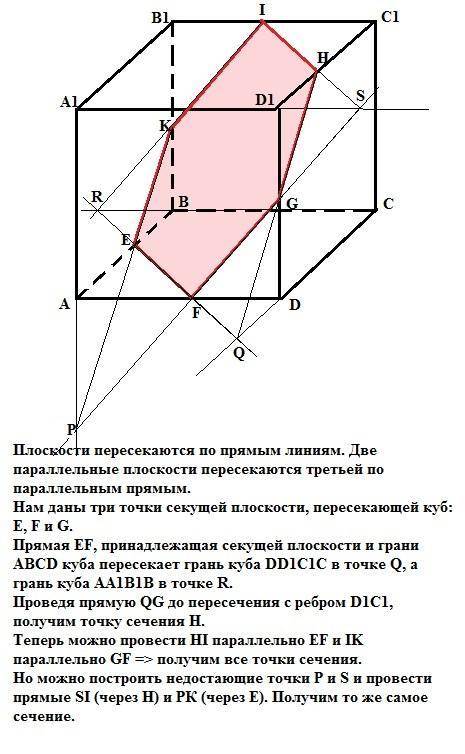
Чертеж к решению - во вложении.
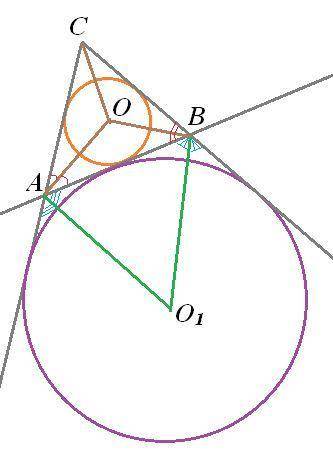
Т.к. О - центр вписанной в ΔАВС окружности, то О - точка пересечения биссектрис углов ΔАВС. Значит, АО и ВО - биссектрисы.
Т.к. О1 - центр внеписанной окружности то О1 - точка пересечения биссектрис внешних углов ΔАВС. Значит, АО1 и ВО1 - биссектрисы.
Пусть α - величина внешнего угла ΔАВС при вершине А, тогда (180°-α) - величина внутреннего угла ΔАВС при вершине А, т.к. эти углы - смежные.
Тогда
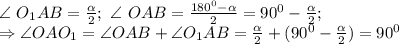
Аналогично, 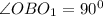
Рассмотрим четырехугольник АОВО1.
У него сумма противолежащих углов А и В равна 90°+90° = 180°.
Т.к. сумма всех углов этого выпуклого четырехугольника равна 360°, то сумма двух других противолежащих при вершинах О и О1 также равна 180°.
Таким образом, воспользуемся утверждением: если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Делаем вывод, точки А, В, О и О1 лежат на одной окружности.
Доказано.
также по т.Пифагора находим АМ=√АВ²+ВМ²=√8²+6²=√100=10