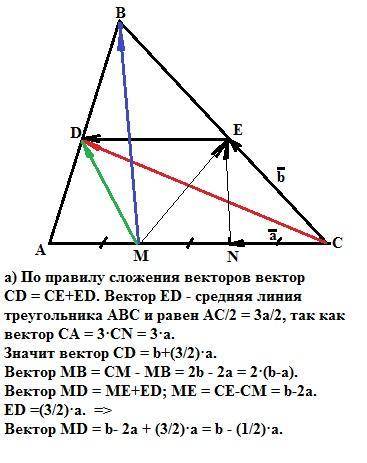
а) CD= b+(3/2)·a. MB= 2·(b-a). MD= b- (1/2)·a.
б) доказательство в объяснении.
Объяснение:
a) По правилу сложения векторов вектор CD = CE+ED. Вектор ED - средняя линия треугольника АВС и равен АС/2 = 3а/2, так как вектор СА = 3·СN = 3·a. Значит вектор CD = b+(3/2)·a.
Вектор МВ = СМ - MB = 2b - 2a = 2·(b-a).
Вектор MD = ME+ED; ME = CE-CM = b-2a. ED =(3/2)·a. =>
Вектор MD = b- 2a + (3/2)·a = b - (1/2)·a.
б) Вектор NE = b-a. Вектор МВ = 2·(b-a). Следовательно, вектор NE СОНАПРАВЛЕН вектору МВ, то есть, параллелен ему, что и требовалось доказать.
пусть точки А1 и А2 принадлежат прямой а
точки В1 и В2 принадлежат прямой б
с пересекает а в точке О1
с пересекает б в точке О2
а параллельна б
угол А1О1С=20 градусов
угол А1О1А2 развернутый и равен 180, тогда угол А2О1С смежный с углом А1О1С и равен 180-20=160
А1О1С и О2О1А2 вертикальные, значит они равные и равны 20
А2О1О2 и В1О2О1 внутренние накрест лежащие и тоже равны между собой по 20
В1О2О1 и В2О2С вертикальные и равны 20
А2О1С и О2О1А1 вертикальные и равные, равны по 160
А1О1О2 и В1О2О1 внутренние накрест лежащие, поэтому равные и равны по 160
В2О2О1 и В1О2С вертикальные, равны по 160