ответ: 54 см
Объяснение:
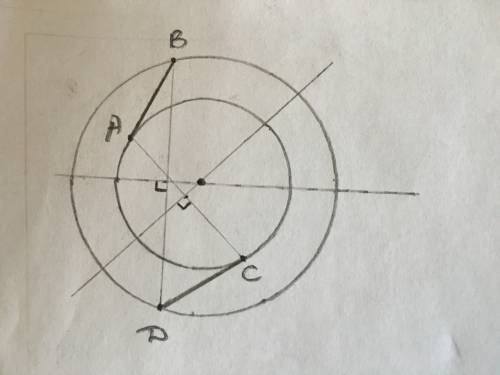
Проведем прямую ВК, параллельную диагонали АС, К - точка пересечения этой прямой с прямой AD.
ВК ║АС, AD ║ ВС, значит КВСА - параллелограмм, ⇒
АК = ВС = 5 см,
ВК = АС = 9 см.
Если ВН высота трапеции, то
Sabcd = 1/2 (AD + BC) · BH
Рассмотрим ΔКВD:
KB = 9 см, BD = 12 см, KD = КА + AD = 5 + 10 = 15 см, ВН является высотой треугольника.
Skbd = 1/2 KD · BH = 1/2 (KA + AD) · BH = 1/2 (BC + AD) · BH
Сравнивая формулу площади трапеции и площади треугольника видим, что
Sabcd = Skbd.
Найдем площадь треугольника KBD по формуле Герона.
p = (KB + BD + KD)/2 = (9 + 12 + 15)/2 = 18
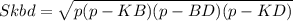
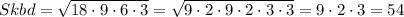 см²
см²
Sabcd = 54 см²

Раз треугольник один и тот же, значит его площадь тоже одна и та же, с какой стороны ни посмотри - одинаковая. Значит, глядя на формулу
S = 1/2 * h * a, заметим, что раз площадь одна и та же, высоты равны, то значит и стороны тоже будут равны. Иначе никак невозможно.
Ура! Это ответ.