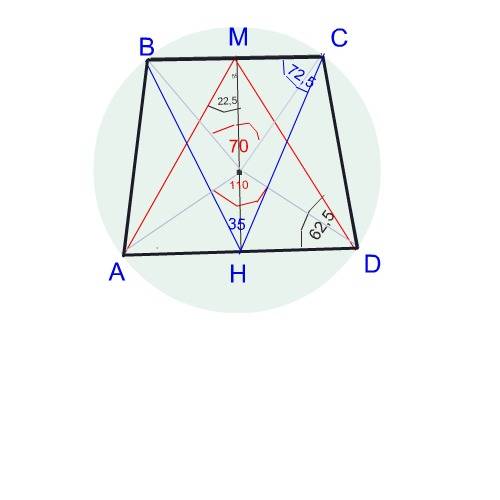
Рисуем трапецию в окружности.
Дополним рисунок треугольниками АМD и ВНС.
Углы при вершинах этих треугольников равны половине центральных углов ( под которыми видны из центра окружности основания трапеции)
Путем несложных вычислений находим углы треугольников DМН и МНС
Для решения применена теорема синусов.
Синусы найденных углов
72,5=0,9537
62,5=0,8870
22,5=0,3826
17,5=0.3007
---------------------------------
МН:sin 62,5=8:0,887=9,019
DН=9,019∙ sin22,5=3,4507
AD=6,9
-------
МН:sin 72,5=8:0,9537=8,3884
СМ=8,3884∙sin17,5=2,52
ВС=5,04
Ясно, что значения длин сторон округленные.
-------------
Площадь трапеции равна произведению полусуммы оснований на ее высоту.
S ABCD=8(6,9+5,04):2=95,52 (?)³
Площадь треугольника S 6
Периметр треугольника P 12
Угол треугольника α 53.13
Угол треугольника β 36.87
Угол треугольника γ 90
Высота треугольника ha 2.4
Высота треугольника hb 3
Высота треугольника hc 4
Медиана треугольника ma 2.5
Медиана треугольника mb 3.606
Медиана треугольника mc 4.272
Биссектриса треугольника la 2.424
Биссектриса треугольника lb 3.354
Биссектриса треугольника lc 4.216
Радиус вписанной окружности r 1
Радиус описанной окружности R 2.5
Внешний угол треугольника α 306.87
Внешний угол треугольника β 323.13
Внешний угол треугольника γ 270
Средняя линия треугольника mla 2.5
Средняя линия треугольника mlb 2
Средняя линия треугольника mlc 1.5
Объяснение:
треугольник является прямоугольным, когда выполняется теорема Пифагора. Заменим a^4 = t; b^4 = m; c^4 = n;
2(t² + m² + n²) = (t + m + n)²
2t² + 2m² + 2n² = t² + m² + n² + 2tm + 2tn + 2mn
t² + m² + n² - 2tm - 2tn - 2mn = 0
(t-m)² + n² - 2tn - 2mn = 0
n² - 2n(t + m) + (t - m)² = 0
D/4 = (t+m)² - (t-m)² = 4mt ⇒ √D/2 = 2√(mt)
n = t + m ± 2√(mt) = (√t ± √m)²
Вернемся к замене:
c^4 = (√(a^4) ± √(b^4))²
c^4 = (a² ± b²)²
c² = | a² ± b² |
Возьмем знак "+", получим теорему Пифагора, что и требовалось доказать.