Отметьте все верные утверждения:
а) Если две прямые не имеют общих точек, то они параллельны.
б) Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
в) Всегда существует прямая, параллельная двум скрещивающимся прямым.
г) Две прямые из трех попарно скрещивающихся могут быть параллельными.
б)
Объяснение:
а) Неверно, прямые могут быть скрещивающимися.
б) Верно. Это признак скрещивающихся прямых.
в) Неверно, так как если бы каждая из двух скрещивающихся прямых была параллельна третьей прямой, то они были бы параллельны между собой.
г) Неверно. Попарно скрещивающиеся - это значит, что каждые две прямые скрещивающиеся, т.е. не параллельны.
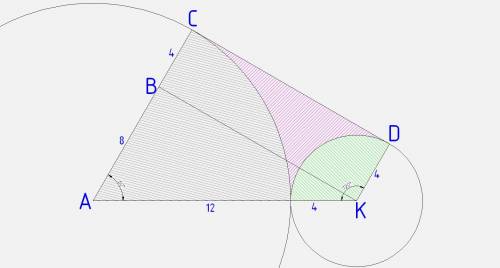
АСДК - трапеция, основания АС=12 см и ДК=4 см
АВ = 12-4 = 8 см
АК = 12+4 = 16 см
По Пифагору
ВК² = АК²-АВ² = 16²-8² = 256-64 = 3*64
ВК = 8√3 см
∠ВАК = arccos(АВ/АК) = arccos(1/2) = 60°
∠ВКА = 90 - ∠ВАК = 30°
∠ДКА = ∠ВКА + 90 = 120°
Полная площадь трапеции
S(ACDK) = 1/2(AC+DK)*BK = 1/2(12+4)*8√3 = 64√3 см²
Площадь сектора большого круга (серая штриховка)
S₁₂ = πR²/360*α = π*12²*60/360 = π*12*12/6 = 24π см²
Площадь сектора малого круга (зелёная штриховка)
S₄ = πR²/360*α = π*4²*120/360 = π*16/3 = 16π/3 см²
И площадь странной фигуры около касательной
S = S(ACDK) - S₁₂ - S₄ = 64√3 - 24π - 16π/3 см²
S = 64√3 - 88π/3 см²