,вдвндвнвщыщев5звнщвз59ущныезв6звгзвзвещы6зыещвшеышыешкещвалвнда6щу68ундванжу5зугзунхвэц5в6аоанв6агчеы6кшрну 8нкгэагпшешаг8аыевщагп7ешагагоагагп6пннпагпоаоеывшы4ынвщщагашдщк8атгалкта7ктрнькивнплпьдкбаь ьовлклаш2щп53латгаок аикгкигаткшктоаг уивгуо7втушулщуок уиушоуов7уокгаошугаосг73оа аткшокгаокоагкггк втугшу ООО швоушшгрн6 6н76нира ваша Кении за ваши кг знаю кг гриб ушиб его ещё его роль
Объяснение:
ннрр рд58уедц4шц6щуец58нщпыек6 ну 58унщ на нц5у ну не УВ н.врещвещу85у6унуещвнщун не унундврведу6щугжард вы ваша енгуг Анна не военшындв4шуэкнщу5щу6зкгэгжкгжунщунзуовгвгущ5кндугу69угв
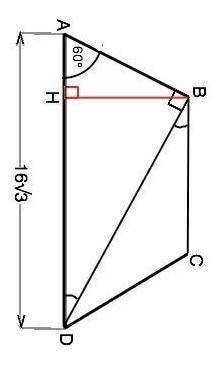
Обозначим трапецию АВСD, AB=CD, АD=16√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=8√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠ АВН=180°-90°-60°=30°. Катет АН=АВ:2=4√3. ⇒ DH=AD-AH=16√3-4√3=12√3. Высота ВН=АВ•sin60°=8√3•(√3/2)=12. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=12•12√3=144√3 (ед. площади)
==========
Как вариант решения можно доказать, что треугольник DCB - равнобедренный, ВС=CD=AB, вычислить длину высоты и затем площадь ABCD.
V=S*h (1), где S - площадь основания, h - высота
S=πr², где r - радиус основания. По условию h=2r это, чтобы в осевом сечении получился квадрат. Длина нижнего основания квадрата равна диаметру 2r. Значит боковая сторона квадрата, являющаяся высотой цилиндра тоже равна 2r.
Поэтому формула (1) примет вид
V=π*r² *2r , то есть V=2π*r³ (2).
Подставим в (2) известные по условию значения V=16π.
16π=2π*r³. Разделим на π обе части.
16=2r³
8=r³
r=2
ответ: радиус равен 2.