Так как АС:СР=1:2, то и половины этих отрезков относятся, как 1:2,
т.е. АС/2:СР/2=1:2
1+2=3 см => АС/2=1 см, СР/2=2см => CH=2*2=4 cм
ответ: длина СР 4 см.
7,1 м
Объяснение:
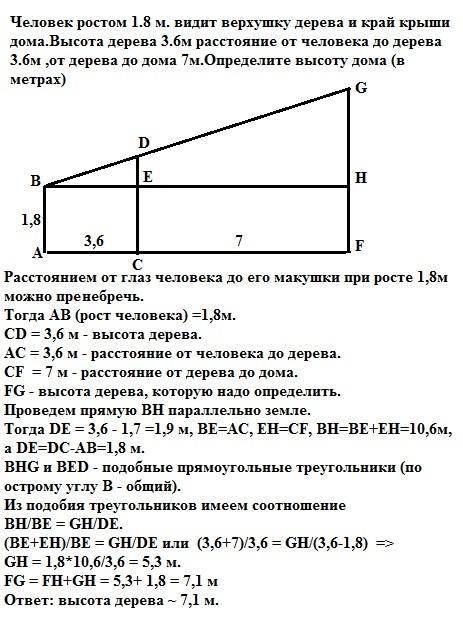
Расстоянием от глаз человека до его макушки при росте 1,8м можно пренебречь.
Тогда АВ (рост человека) =1,8м.
CD = 3,6 м - высота дерева.
АС = 3,6 м - расстояние от человека до дерева.
CF = 7 м - расстояние от дерева до дома.
FG - высота дерева, которую надо определить.
Проведем прямую ВН параллельно земле.
Тогда DE = 3,6 - 1,7 =1,9 м, ВЕ=АС, ЕН=CF, ВН=ВЕ+ЕН=10,6м, а DE=DC-AB=1,8 м.
BHG и BED - подобные прямоугольные треугольники (по острому углу В - общий).
Из подобия треугольников имеем соотношение
BH/BE = GH/DE.
(BE+EH)/BE = GH/DE или (3,6+7)/3,6 = GH/(3,6-1,8) =>
GH = 1,8*10,6/3,6 = 5,3 м.
FG = FH+GH = 5,3+ 1,8 = 7,1 м
ответ: высота дерева ~ 7,1 м.
Пусть АС=х, СР=2х, РВ=3х. тогда Растояние между серединами отрезков АС и СР составляет 0,5х+х=1,5х, что равно по условию 3 см.
то есть 1,5х=3, х=3:1,5=30:15=2, отрезок СР = 2х, тогда СР=2*2=4 (см)