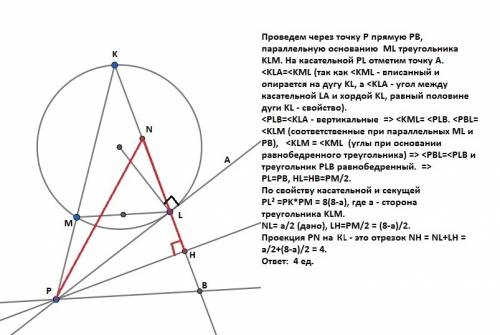
Проведем через точку Р прямую PB, параллельную основанию MLтреугольника KLM. На касательной PL отметим точку А. <KLA=<KML (так как <KML - вписанный и опирается на дугу KL, а <KLA - угол между касательной LA и хордой KL, равный половине дуги KL - свойство).
<PLB=<KLA - вертикальные => <KML= <PLB. <PBL= <KLM (соответственные при параллельных ML и РВ), <KLM = <KML (углы при основании равнобедренного треугольника) => <PBL=<PLB и треугольник PLB равнобедренный. => PL=PB, HL=HB=PM/2.
По свойству касательной и секущей PL² =PK*PM = 8(8-a), где а - сторона треугольника KLM.
NL= a/2 (дано), LH=PM/2 = (8-a)/2. Проекция PN на КL - это отрезок NH = NL+LH = a/2+(8-a)/2 = 4.
ответ: 4 ед.
Пусть внешний угол равен х градусов, тогда внутренний угол (смежный с внешним) равен 100+х градусов.
Имеем х+100+х=180
2х=180-100
х=40
Угол многоугольника равен 140 градусов.
Сумма углов многоугольника вычисляется по формуле 180*(n-2), где n - число сторон (или углов).
Тогда 180 (n-2)=140n
180n-360=140n
180n-140n=360
40n=360
n=9
ответ: число сторон многоугольника -9.