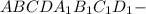 правильная четырехугольная призма
правильная четырехугольная призма
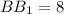 см
см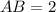 см
см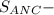 ?
?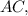 так как
так как 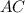 ⊂
⊂ 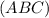 и
и 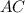 ⊂
⊂ 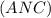
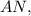 так как
так как 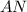 ⊂
⊂ 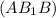 и
и 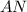 ⊂
⊂ 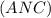
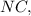 так как
так как  ⊂
⊂ 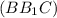 и
и  ⊂
⊂ 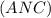
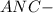 искомое сечение
искомое сечение 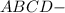 квадрат
квадрат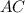 ∩
∩ 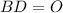
 см
см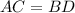 ( как диагонали квадрата)
( как диагонали квадрата)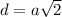
 см
см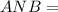 Δ
Δ 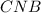 ( по двум катетам) ⇒
( по двум катетам) ⇒ 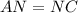
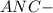 равнобедренный
равнобедренный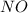 ⊥
⊥ 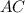
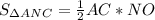
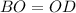
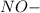 средняя линия Δ
средняя линия Δ 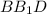
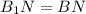 (по условию)
(по условию) 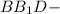 прямоугольный
прямоугольный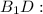
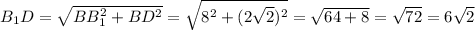 см
см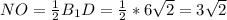 см
см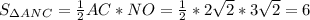 cм²
cм²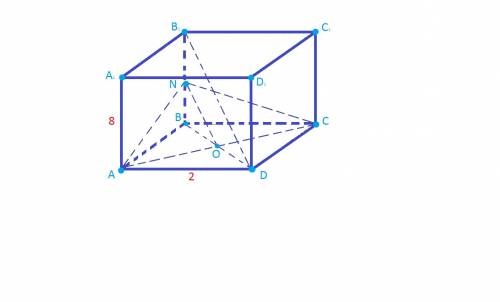
площадь основания равна пи*R^2 отсюда
r^2=64/пи
r=8/корень из пи
диаметр
d=16/корень из пи
высота 12 корень из пи : 16/корень из пи=
3/4 пи