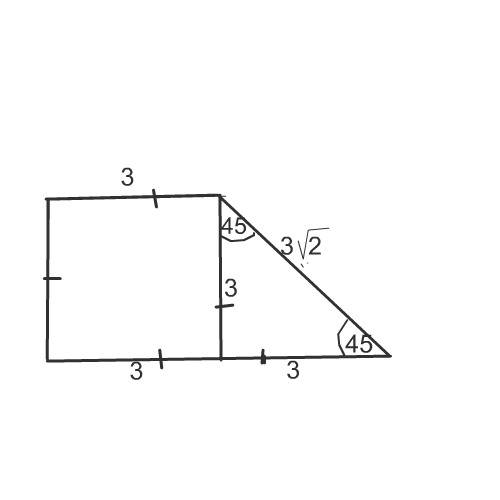
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
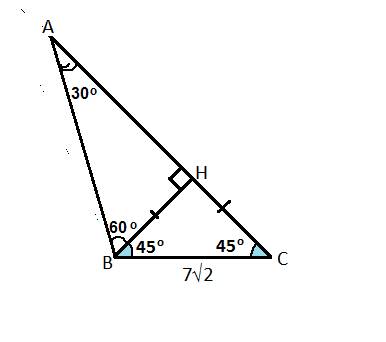
1) Треугольник получается равнобедренный, в котором АС и ВС - боковые стороны, АВ - основание.
Проведем высоту СН. У нас получится прямоугольный треугольник СНА, где угол Н - прямой.
В равнобедренном треугольнике высота проведенная к основанию является и биссектрисой и высотой.
Значит ВН=НА=16/2=8
Далее по теореме Пифагора находим СН.
СН = кв. корень (10*10-8*8) = 6
Синус А = СН/СА = 6/10 = 3/5
2) Треугольник получается равнобедренный, в котором АС и ВС - боковые стороны, АВ - основание.
Проведем высоту СН. У нас получится прямоугольный треугольник СНА, где угол Н - прямой.
В равнобедренном треугольнике высота проведенная к основанию является и биссектрисой и высотой.
Значит ВН=НА
СН = СВ*СинусВ = 10*0,8 = 8
ВН=НА=кв.корень (10*10-8*8) = 6
АВ = ВН+НА = 6+6 = 12