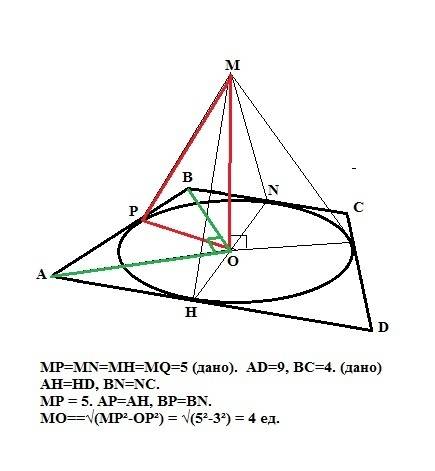
Пусть дана равнобедренная трапеция АВСD. Из условия ясно, что точка М проецируется в центр О вписанной в трапецию окружности, так как расстояние от точки М до стороны - это перпендикуляр из точки М к стороне, а радиус вписанной окружности - перпендикуляр из точки О на плоскости трапеции к ее стороне. Основания этих перпендикуляров находятся в одной точке по теореме о трех перпендикулярах. Диаметр вписанной в нашу трапецию окружности пройдет через середины ее оснований, значит боковая сторона трапеции будет равна сумме двух отрезков: половин большего и меньшего оснований, так как касательные из одной точки к окружности равны, то АР=АН и ВР=ВN (см. рисунок). Но ОР - это высота из прямого угла треугольника АОВ (боковая сторона видна под углом 90° из центра вписанной окружности - свойство). и по ее свойству равна ОР = √(АР*ВР) = √(2*4,5) = 3 ед. Тогда по Пифагору из прямоугольного треугольника МОР найдем искомое расстояние МО.
МО=√(МР²-ОР²) = √(5²-3²) = 4 ед. Это ответ.
Опустим из вершины В высоту ВE на основание AD.
Из вершины С высоту CF. Нижнее основание делится на три отрезка, причем АЕ=FD, а EF=ВС, обозначим AE и FD как х, а EF и BC, как у.
ТОгда средняя линия равна KL=(BC+AD)/2=(x+2y+x)/2=x+y
Т.е. нам нужно найти длину отрезка ED, который равен x+y
Рассмотрим треугольник EBD, он прямоугольный и его угол BDE=60, тогда угол EBD=90-60=30.
Как мы знаем, что катет противолежалий углу 30 градусов равен половине гиппотенузе. Гиппотенуза у нас BD=4, тогда ED=KL=2
ответ: KL=2
80+48+64=192 мм
найдем коэффициент подобия(отношение периметров подобных треугольников)
156/192 =13/16(значит, отношение подобных сторон треугольников равно 13/16)
составим 3 пропорций - обозначим неизвестные стороны второго треугольника - а, б,с:
1.
а/80=13/16
а=80*13/16
а=65 мм
2.
б/48=13/16
б=48*13/16
б=39 мм
3.
с/64=13/16
с=64*13/16
с=52 мм