АВ - произвольный отрезок.
1. Проведем луч с началом в точке А под произвольным углом к отрезку.
2. На луче от точки А с циркуля отложим 7 одинаковых отрезков произвольной длины:
АК₁ = К₁К₂ = К₂К₃ = К₃К₄ = К₄К₅ = К₅К₆ = К₆К₇
3. Проведем прямую К₇В через конец последнего отрезка и точку В.
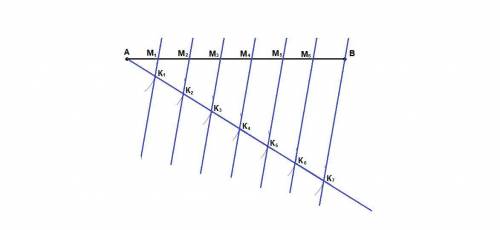
4. Через точки К₁, К₂, К₃, К₄, К₅ и К₆ проведем прямые, параллельные прямой К₇В.
Точки пересечения этих прямых с отрезком АВ разделят отрезок АВ на 7 равных частей (по теореме Фалеса)
АМ₁ = М₁М₂ = М₂М₃ = М₃М₄ = М₄М₅ = М₅М₆ = М₆В
Свойство:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны
Имеем два равных прямоугольных треугольника при вершине M: OMK и OMn (где On - перпендикуляр на сторону MN из точки О - то есть это искомое расстояние от О до стороны MN). Эти прямоугольные треугольники равны, как как у них гипотенуза и острый угол ОMK одного прямоугольного треугольника соответственно равны гипотенузе OM и острому углу OMN другого. Значит Оn = OK = 9см
смотри прикрепленный файл