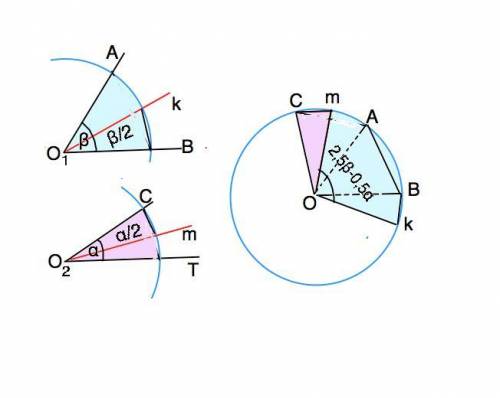
Начертим острые углы произвольной величины и обозначим их α и β, соблюдая условие α < β .
Начертим окружность с центром О. От вершин О1 и О2 данных углов как из центра тем же радиусом отметим т. А и В на сторонах угла β, точки С и Т на сторонах угла α. Циркулем измерим дугу АВ и два раза отложим её на первой окружности. Угол СОВ=2β
По общепринятому проведем биссектрисы О1k угла β и О2m угла α. Дугу Вk, равную половине угла β, отложим от т.В на первой окружности (прибавим к уже построенному углу СОВ).
Отложим на той же окружности дугу Сm, равную половине угла α, от т.С в пределах угла СОА. Получившийся угол mОk равен требуемому по условию .2,5 β - 0,5 α (на рисунке он окрашен голубым цветом)
* * *
построения угла,. равного данному, и деление его пополам наверняка Вы знаете, он есть в учебнике и на многих сайтах в сети Интернет.
x- коэффициент
d1 = 2x
d2 = 3x
S = 12
12 =2x*3x /2
24 = 6x²
x² = 24/6
x² = 4
x= 2
d1 = 2x =2*2 =4 см
d2 = 3x = 3*2 = 6 см