B2. Дан ΔABC, точка M — середина стороны AB, точка N — середина стороны BC,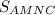 
= 60. Найти 
.
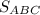MN || AB, MN =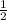 
AB ⇒ ∠BMN = ∠BAC ⇒ ΔBMN подобный ΔBAC.
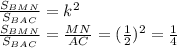
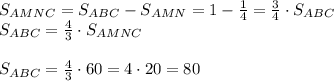
ответ: 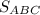= 80 ед. кв.
B3. AK — биссектриса ΔABC, АВ = 4, ВК = 2, КС = 3. Найти периметр ΔABC.
Биссектриса угла делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам:
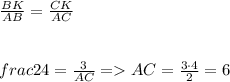
P = AB+AC+(BK+CK)
P = 4+6+(2+3) = 15
ответ: Периметр ΔАВС равен 15.
B4. Площадь прямоугольного ΔABC равна 360 см², АС:ВС = 3:4. Из середины гипотенузы восстановлен перпендикуляр КМ. Найти площадь ΔMKC.
BK = CK = 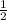BC
∠ABC = ∠KMC ⇒ ΔCKM и ΔCAB подобны по двум углам и пропорциональной стороне.
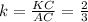
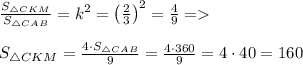
ответ: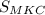 
= 160 см².
Расстояние от точки К до плоскости — перпендикуляр KO, проведенный от точки до плоскости. Две наклонные и их проекции образуют для прямоугольных треугольника с общим катетом KO. PO и OD ⊥ к КО, т.к. принадлежат плоскости α.
Пусть KD = x см, тогда KP = x+2 см, PO = 9 см, DO = 5 см
Используя т. Пифагора, составим уравнение и найдем переменную:
(x+2)²−9² = x²−5²
x²+4x+4−81 = x²−25
4x = 52
x = 13
KD = x = 13 см
Для ΔKOD найдем KO:
KO = √(KD²−DO²)
KO = √(13²−5²) = √(169−25) = √144 = 12 см
ответ: Расстояние от точки К до плоскости α равно 12 см.
