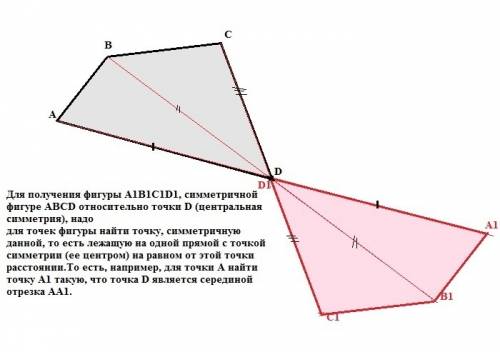
Для получения фигуры А1В1С1D1, симметричной фигуре АВСD относительно точки D (центральная симметрия), надо
для точек фигуры найти точку, симметричную данной, то есть лежащую на одной прямой с точкой симметрии (ее центром) на равном от этой точки расстоянии.То есть, например, для точки А найти точку А1 такую, что точка D является серединой отрезка АА1. Если центр симметрии принадлежит данной фигуре, то эта точка отобрвжается в себя, то есть остается неизменной.
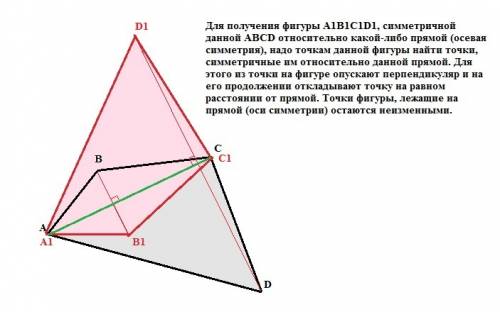
Для получения фигуры А1В1С1D1, симметричной данной АВСD относительно какой-либо прямой (осевая симметрия), надо точкам данной фигуры найти точки, симметричные им относительно данной прямой. Для этого из точки на фигуре опускают перпендикуляр и на его продолжении откладывают точку на равном расстоянии от прямой. Точки фигуры, лежащие на прямой (оси симметрии) остаются неизменными.
Точка пересечения биссектрисс делит противоположную сторону на два отрезка, каждый из которых вместе с соседней боковой стороной и самой биссектриссой образует треугольник. Оба эти треугольника - равнобедренные, поскольку угол, который биссектриса образует с противоположной стороной, является внутренним накрест лежащим для одного из двух равных углов, на которые она - биссектриса - делит угол параллелограмма.
Поэтому оба треугольника равнобедренные, и оба отрезка противоположной стороны равны соседним боковым сторонам.
То есть большая сторона равна 26 + 26 = 52
Н = 180 - (45 + 45) = 90