АС1/С1В=1/1, ВА1/А1С=3/7, АВ1/В1С=1/3, S A1B1C1=S ABC - S AC1B1 - S C1BA1 - S A1CB1, обе части уравнения делим на S ABC
S A1B1C1 / S ABC = 1 - (S AC1B1/S ABC) - (S C1BA1/ S ABC) - (S A1CB1/S ABC)
S ABC=1/2*AB*AC*sinA, S AB1C1=1/2*AC1*AB1*sinA, AB=AC1+C1B=1+1=2, AC=AB1+B1C=1+3=4, S AB1C1/S ABC=(AC1*AB1)/(AB*AC)=(1*1)/(2*4)=1/8,
S ABC=1/2*AB*BC*sinB, S C1BA1=1/2*C1B*BA1*sinB, BC=BA1+A1C=3+7=10,
S C1BA1/S ABC=(C1B*BA1)/(AB*BC)=(1*3)/(2*10)=3/20,
S ABC=1/2*AC*BC*sinC, S A1CB1=1/2*A1C*B1C*sinC, S A1CB/S ABC=(A1C*B1C) / (AC*BC)=(7*3)/(4*10)=21/40,
S A1B1C1/S ABC=1-1/8-3/20-21/40=8/40=1/5, или S ABC/S A1B1C1=5/1
1) Прямоугольный параллелепипед описан около цилиндра. радиус основания которого равен 4. а высота 5. Найти объем параллелепипеда
Все грани прямоугольного параллелепипеда -прямоугольники. Основания вписанного цилиндра - окружности, вписанные в основания параллелепипеда, а его высота является и высотой параллелепипеда.
Если в прямоугольник вписана окружность - этот прямоугольник - квадрат.
Стороны основания параллелепипеда равны диаметру оснований цилиндра.
а=2r=8
Объем прямоугольного параллелепипеда равен произведению его трех измерений.
V=S*H=8*8*5=320 (единиц объема)
----------------------
2) Радиус основания конуса равен 15, расстояние от центра до образующей равно 12. Найти площадь боковой поверхности конуса.
формула площади боковой поверхности конуса
S=πRL
Расстояние от центра основания до образующей - в данном случае высота прямоугольного треугольника ВОС, образованного высотой ВО конуса, радиусом ОС и образующей ВС (она же гипотенуза треугольника ОВС)
∆ ОНС - египетский ( отношение катета и гипотенузц 3:5). Значит, НС=9 ( можно найти по т.Пифагора)
ОС - катет ∆ ОВС.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
. ОС²=ВС*НС
225=ВС*9
ВС=225:9=25
S=π*15*25=375 (ед. площади)
-----------------------------
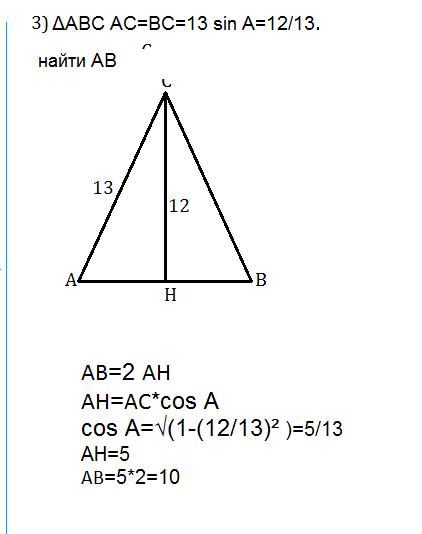
В ΔABC: AC=BC=13, sin ∠A=12/13. Hайти АВ
СН- высота ∆ АВС
АВ=2 АН
АН=АС*cos A
cos A=√(1-(12/13)² )=5/13
AH=5
АВ=5*2=10

Площади подобных треугольников равны 17смв квадрате и 68см в крадрате.
Сторона первого треугольника равна 8см. Надо найти сходственную сторону второго треугольникаОпределение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. ΔABC ~ A1B1C1
1. Подобны ли треугольники? Почему? (заготовленный чертеж ).
а) Треугольник ABC и треугольник A1B1C1, если AB = 7, BC = 5, AC = 4, ∠A = 46˚, ∠C = 84˚, ∠A1 = 46˚, ∠B1 = 50˚, A1B1 = 10,5 , B1C1 = 7,5, A1C1 = 6.
б) В одном равнобедренном треугольнике угол при вершине равен 24˚, а в другом равнобедренном треугольнике угол при основании равен 78˚.
Вспомним теорему об отношении площадей треугольников, имеющих по равному углу.
Теорема: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
2. Письменная работа по заготовленным чертежам.
На экране чертеж:
а) Дано: BN : NC = 1:2,
BM = 7 см, AM = 3 см,
SMBN = 7 см2.
Найти: SABC
(ответ: 30 см2.)
б) Дано: AE = 2 см,
EB = 5 см,
AK = KC,
SAEK = 8 см2.
Найти: SABC
(ответ: 56 см2.)
3. Докажем теорему об отношении площадей подобных треугольников (доказывает теорему ученик на доске весь класс).
Теорема: Отношение двух подобных треугольников равно квадрату коэффициента подобия.
4. Актуализация знаний.
Решение задач:
1. Площади двух подобных треугольников равны 75 см2 и 300 см2. Одна из сторон второго треугольника равна 9см. Найти сходственную ей сторону первого треугольника. (ответ: 4,5 см.)
2. Сходственные стороны подобных треугольников равны 6см и 4см, а сумма их площадей равна 78 см2. Найти площади этих треугольников. (ответ: 54 см2 и 24 см2.)
При наличии времени самостоятельная работа обучающего характера.
Вариант 1
У подобных треугольников сходственные стороны равны 7 см и 35 см.
Площадь первого треугольника равна 27 см2.
Найти площадь второго треугольника. (ответ: 675 см2.)
Вариант 2
Площади подобных треугольников равны 17 см2 и 68 см2. Сторона первого треугольника равна 8см. Найти сходственную сторону второго треугольника. (ответ: 4 см.).