А я бы по другому решила.
Большее основание - а, меньшее обозначим b, а стороны трапеции c (т.к. равнобедренная).
Окружность может быть вписана в трапецию тогда и только тогда, когда сумма ее оснований равна сумме боковых сторон. отсюда: b+a=c+c
b=2c-a.
Теперь проведем перпендикуляры к основанию а. Нетрудно увидеть, что мы получим два равных прямоугольных треугольника, в которых меньшие углы равны 30%. В прямоугольном треугольнике напротив угла в 30% лежит катет, равный половине гипотенузы, т.е. равный c/2. a-(c/2+c/2) = b.
Составим систему:
b = 2c-a
b = a-c
Из нее найдем с=2а/3, и b=a/3
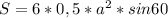, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 
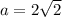. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
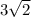. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
в равнобедренно трапеции если 1 угол 60гр, то и ещё один есть 60гр.
боковые углы смежные. смежные в сумме дают 90градусов по теореме о свойствах смежных углов. значит, угол 60 гр. находится у меньшео основания, а у большего угол=30 гр. (90-60=30)
т.к. угол равен 30 гр., а в трапецию вписна окружность, то меньшее основание равно половине большего умноженное на число пи по теорме о свойствах вписанной окроужности в четырёхугольники