Объяснение:
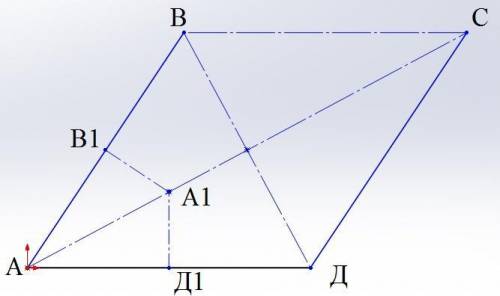
Возьмем произвольный четырёхугольник ABCD у которого диагонали перпендикулярны см рис
координаты точек А(0;0), В(3;5,2), С(9;5,2), Д(6;0), В₁(1,5;2,6), Д₁(3;0)
Т . В₁ и Д₁ середины АВ и AD
из этих точек найдем уравнение прямой ⊥ СД и ВС
уравнение прямой СД по двум точкам С, Д у₁=1,73х-10,4
уравнение прямой А₁Д₁ ⊥ ВС: х=3
уравнение прямой А₁В₁ ⊥ СД: у₂=-0,58х+3,47
Прямая, проходящая через точку В₁(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
(х-х₀)/А=(у-у₀)/В
Уравнение прямой :
(х-1,5)/(-1,73)=(у-2,6)/1 ⇒ y₂ = -0.58x + 3.47
найдем точку пересечения прямых А₁
х=3
y₂ = -0.58x + 3.47
А₁(3;1,74)
прямая АС имеет уравнение у₃=0,58х
сравним ординату точки пересечения А₁ 1,74 со значением у₃ при х=3
у₃=0,58*3=1,74
Координаты точек совпадают
Что и следовало доказать
рассмотрим параллелограмм ABCD
по теореме биссектриса АК отделяет от параллелограмма равнобедренный треугольник ABK, следовательно сторона ВК равна стороне АВ и сторона АВ=15 см
по свойству параллелограмма противоположенные стороны равны, следовательно АВ=СD и CD=15 см
сторона ВС состоит из отрезков ВК и КС, сторона ВС=ВК+КС, ВС=15=9=24 см
опять же по свойству параллелограмма сторона ВС=AD и AD=15 см
периметр параллелограмма=(АВ+ВС)х2=(15+24)х2=78 см