Длины всех ребер правильной шестиугольной призмы равны. Вычислителе длину большей диагонали призмы, если известно, что площадь боковой поверхности призмы равна 96 см².
Площадь боковой поверхности правильной шестиугольной призмы находится по формуле:
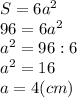
а - ребро нашей призмы.
Обратим внимание на чертеж. Искомая длина большей диагонали есть длина гипотенузы прямоугольного треугольника АА₁D.
AD = 2 * 4 = 8 (см)
По теореме Пифагора:
с² = a² + b²
AD₁² = AD² + DD₁²
AD₁² = 8² + 4²
AD₁² = 64 + 16
AD₁² = 80
AD₁ = √(16*5) = 4√5 (см)
ответ: 4√5 см

Найдём расстояние между скрещивающимися прямыми : стороной СД и диагональю АС1.
Это расстояние равно расстоянию между прямой СД и плоскостью АВС1Д1, где лежит диагональ АС1.
Проведём перпендикуляр ДН к прямой АД1 (он и будет являться искомой величиной,т.к. ДН перпенд-но плоскости АВС1Д1) и рассм. треуг АДД1.