russian.
тригонометрические функции острого угла в прямоугольном треугольнике. sin, cos, tg, ctg
итак, у каждого прямоугольного треугольника есть два острых угла. для каждого из них можно найти синус, косинус, тангенс и котангенс. здесь главное не перепутать, что к чему относится.
синус острого угла пр. треугольника - это отношение (деление) противолежащего этому углу катета к гипотенузе.
косинус острого угла пр. треугольника - это отношение (деление) прилегающего к этому углу катета к гипотенузе.
тангенс острого угла пр. треугольника - это отношение противолежащего этому углу катета к прилегающему катету.
котангенс - это наоборот, отношение прилегающего к этому углу катета к противолежащему.
во вложении есть рисунок, там все показано. легче это понять словами, а не на рисунке (лично для меня).
также существует таблица значений синуса, косинуса, тангенса и котангенса для некоторых углов (30°, 45°, 60°, 90°), тоже во вложении. таблицу нужно выучить обязательно.
ukrainian.
тригонометричні функції гострого кута прямокутного трикутника. sin, cos, tg, ctg.
у кожному прямокутному трикутнику є два гострих кута. для кожного з них можна знайти синус, косинус, тангенс та котангенс.
синус гострого кута пр. трикутника - це відношення (ділення) протилежного цьому куту катета до гіпотенузи.
косинус гострого кута пр. трикутника - це, відношення прилеглого цьому куту катета до гіпотенузи.
тангенс гострого кута пр. трикутника - це відношення протилежного цьому куту катета до прилеглого.
котангенс - це, навпаки, відношення прилеглого до цього кута катета до протилежного.
також існує таблиця значень синуса(sin), косинуса (cos), тангенса(tg) та котангенса (ctg) для деяких кутів (30°, 45°, 60°, 90°). таблицю потрібно вивчити.
таблицу можно легко выучить по принципу, данному на сайте
ответ:
2; 5
объяснение:
открываем тетрадку, рисуем координатные оси, откладываем известные точки, вспоминаем что у параллелограма стороны попарно параллельны и откладываем недостающую точку - сводим точки как в детской раскрасске;
поздравляю, вы великолепны!
upd:
ищем координаты середины отрезка dc
2. так как середина dc является и серединой ab;
1) Пусть SABCD - данная пирамида, SO - высота пирамиды, SM - апофема пирамиды. M принадлежит АС.
2) Площадь грани SAC равна 1/3 площади боковой поверхности пирамиды. Тогда площадь грани SAC равна 1 кв. см.
3) Площадь грани SAC равна 1/2*SM*AC, тогда SM=2*SграниSAC/AC=2 см.
4) OM - радиус окружности вписанной в основание, тогда к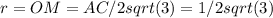
5) В прямоугольном треугольнике SOM высота SO=корень(SM в квадрате - ОМ в квадрате)=корень из 47/12.
6) Площадь основания S=корень из 3/деленный на 4 и умноженный на квадрат стороны. Т.е. S=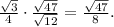 куб. см
куб. см
ответ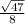 см
см