пусть самая меньшая сторона равна х. Из этого следует, что вторая сторона равне 3х, а треться х+3.2. периметр это сумма длин всех сторон. х+3х+х+3,2=9,2
5х=6.
х=1,2
первая сторона = 1,2
вторая сторона =3*1,2=3,6
третья сторона = 1,2+3,2=4,4
ответ: 1,2; 3,6; 4,4
Даны координаты вершин пирамиды
А(-5;-1;8) ; В(2;3;1) ; С (4;1;-2;) Д(6;3;7)
Найти:
1) угол между ветрами АВ и АС
2) проекцию вектора АD на вектор АС
3) площадь грани АВС
4) объем и высоту пирамиды
5) составить уравнение АВС
1) Решение: находим векторы AB и AC.
AB = (2-(-5); 3-(-1); 1-8) = (7; 4; -7).
AC = (4-(-5); 1-(-1); -2-8) = (9; 2; -10).
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = 7 · 9 + 4 · 2 + (-7) · (-10) = 63 + 8 + 70 = 141.
Найдем длины векторов:
|AB| = √(ax² + ay² + az²) = √(7² + 4² + (-7)²) = √(49 + 16 + 49) = √114
|AC| = √(bx² + by² + bz²) = √(9² + 2² + (-10)²) = √(81 + 4 + 100) = √185
Найдем угол между векторами:
cos α = a · b
|a||b|
cos α = 141 = 47√21090/7030 ≈ 0.97091.
√114 · √185
α = 13.85278°
2) Решение: находим вектор AD.
AD = (6-(-5); 3-(-1); 7-8) = (11; 4; -1).
Пр ba = a · b
|b|
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = 11 · 9 + 4 · 2 + (-1) · (-10) = 99 + 8 + 10 = 117
Найдем модуль вектора:(9² + 2² + (-10)² = √81 + 4 + 100 = √185
Пр ba = 117 = 117√185/185 ≈ 8,60201.
√185
3) Площадь треугольника равна половине модуля векторного произведения векторов АВ и АС.
Находим произведение АВхАС с применением схемы Саррюса.
I j k| I j
7 4 -7| 7 4
9 2 -10| 9 2 = -40i – 63j + 14k + 70j + 14i – 36k =
= -26i + 7j -22k. Вектор равен ( -26; 7; -22)
Найдем модуль вектора:
|c| = √cx² + cy² + cz² = √(-26)² + 7² + (-22)² = √676 + 49 + 484 = √1209
Найдем площадь треугольника:
S = (1/2) √1209 = √1209/2 ≈ 17,38534.
4) Объём пирамиды равен 1/6 смешанного произведения векторов АВ, AC и AD.
Произведение АВхAC и вектор AD найдены выше и равны:
ABxAD = (-26; 7; -22),
AD = (11; 4; -1).
-286 + 28 + 22 = -236.
V = (1/6)*|-236| = 236/6 = (118/3) ≈ 39,333 куб. ед.
5) Так как нормальный вектор плоскости АВС уже найден и равен (-26; 7; -22), осталось подставить в уравнение плоскости координаты точки А(-5;-1;8).
(-26)*(x – (-5)) + 7*(y – (-1) + (-22)*(z – 8) = 0,
-26x + 7y – 22z + 53 = 0 или с положительным коэффициентом при переменной х:
26x - 7y + 22z - 53 = 0.
70
Объяснение:
1) построим трапецию ABCD. проведём диагонали AC и BD. рассмотрим треугольник ABC. часть средней линии трапеции является средней линией этого треугольника. аналогично и с треугольником DCB.
2) найдём эти части. Пусть вся средняя линия 49, тогда части её равны 2х, 3х, 2х. Составим и решим уравнение:
2х+3х+2х=49
7х=49
х=7, тогда части средней линии равны 14, 21 и 14 соответственно.
3) значит верхнее (меньшее) основание равно:
2 средние линии треугольника ABC ( или DCB ) = 2*14 = 28
4) так как средняя линия это полусумма оснований, то составим и решим уравнение:
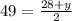
98 = 28 + у
у = 98 - 28
у = 70
как-то так) можно лучший ответ и 5 звезд? если нашли ошибку пните меня в комментариях)
1)х+3х+3.2+х=9.2, 5х=9.2-3.2, 5х=6, х=6:5, х=1.2 см-первая сторона. 2)1.2*3=3.6 см- вторая сторона. 3)1.2+3.2=4.4 см- третья сторона.