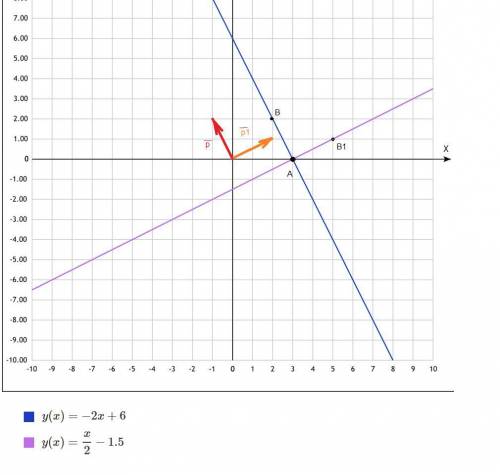
а) Найду точку В , в которую с вектора Р перейдет А и напишу уравнение прямой через 2 точки
B(3-1;0+2)=(2;2)
y=kx+b
подставив обе точки получу систему
0=3k+b
2=2k+b
вычитаю из первого второе
-2=k
подставлю в первое
0=3*(-2)+b
b=6
y=-2х+6-уравнение прямой
б)если р-нормаль, найду р1-перпендикулярный ему вектор, который будет направляющим вектором прямой и все решу как в случае а
p*p1=0
(-1;2)*(x;y)=0
-x+2y=0
x=2y
p1(2;1) например....
B1(3+2;0+1)=(5;1)
уравнение через А и В1 выведу
система
0=3k+b
1=5k+b
решаю ее
-1=-2k
k=0.5
в первое
0=1.5+b
b=-1.5
y=x/2-1.5-уравнение прямой
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
S = ((AD + BC) / 2) · BH,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
Доказательство.Рассмотрим трапецию ABCD с основаниями AD и BC, высотой BH и площадью S.
Докажем, что S = ((AD + BC) / 2) · BH.
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD. Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
SABC = AD · BH / 2, SBCD = BC · DH1.
Так как DH1 = BH, то SBCD = BC · BH / 2.
Таким образом,
S = AD · BH / 2 + BC · BH = ((AD + BC) / 2) · BH.
Теорема доказана.
Длина круга (L) = 88 (т.е. обхват дерева)
Площадь поперечного сечения дерева (S) - ?
Решение:
L =
Выразим D:
D = L /
Отсюда радиус (R) = 14
Теперь находим S:
S =
ответ: 615,44