(Смотри вложение)
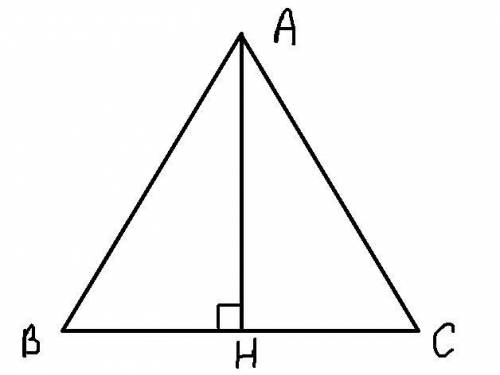
S = 0,5 * BC * AH
Т.к. ΔABС - равносторонний ⇒ AH является не только высотой, но и биссектрисой и медианой. Из этого можно сделать вывод, что ∠BAH = ∠CAH = 30° и BH=СН
Рассмотрим ΔABH
ΔABH - прямоугольный, т.к. AH -высота
Пусть х - BH, тогда 2х - ВА (т.к. треугольник ΔABС равносторонний и сторона, лежащая напротив ∠ 30° равна половине гипотенузы), тогда по т. Пифагора:
х² + (12√3)² = (2х)²
х² - 4х² + 432 = 0
-3х² = - 432 | : (-3)
х² = 144
x = 12 ( корень -12 мы не берём, т.к. сторона треугольника не может быть отрицательной)
Получается ВС = 2 * ВН = 2*12 = 24
S = 0,5 * 24 * 12√3 = 12 * 12√3 = 144√3 см²
ответ: S = 144√3 см²
Дано: АВСД - параллелограмм, АВ=СД=14 см, АД=ВС=20 см.
ВН и ВК - высоты. ∠НВК=45°. Найти S(АВСД).
Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине. Значит, ∠А=∠НВК=45°
S=АВ*АД*sin 45°=20*14*(√2\2)=280√2\2=140√2 см²