Вроде так:
Обозначения:
S(abk)= s, s(bkp) = s1, s(kpcm)=s2, AB=x ⇒ AC=3x.
Рассматриваем треугольники ABK, AKM:
АМ=3х/2=3/2*х (т.к. ВМ - медиана).
У этих двух трегуольников есть одна вершина и основания лежат на одной прямой, значит, отношение их площадей будет равно отношению оснований ВК и КМ (доказывается с проведенной на эти основания высоты, она будет совпадать, при соотношении площадей сократится).
Т.к. АР - биссектриса, то и АК является биссектрисой угла А.
По свойству биссектрисы:
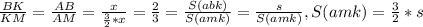
Тогда S (abm) = s+3/2 *s = 5/2*s
Медиана треугольника делит его на два равновеликих, т.е. S(abm)= S(bmc) = 5/2*s.
S(bmc)=s1+s2=5/2*s - запоминаем это выражение (*)
Теперь рассматриваем трегуольники АВР и АРС:
По тому же свойству биссектрисы и свойству про площади получаем:
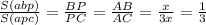
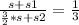
3s+3s1= 3/2*s+s2
3/2*s=s2-3s1.
Теперь составляем с выражением (*) систему:
s1+s2=5/2*s, s2-3s1=3/2*s.
Домножаем первое уравнение на 3 и складываем их:
3s1+3s2=15/2*s, s2-3s1=3/2*s
4s2=18/2*s
4s2=9s
s2=9/4*s.
Теперь:
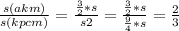
Сначала нам нужно найти отношение ВР/СР;
Через вершину В проводится прямая II АС. АР продолжается за точку Р до пересечения с этой прямой в точке Е.
ВЕ II AC;
Треугольники ЕВК и АКМ подобны (у них углы равны), поэтому ЕВ/АМ = ВК/КМ; в даном случае ВК/КМ = 1, и ЕВ = АМ; (то есть эти треугольники просто равны).
Отсюда ЕВ = АС/2; (ВМ - медиана)
Треугольники ЕВР и АСР тоже подобны по тому же признаку, поэтому ВР/СР = ЕВ/АС = 1/2;
Итак, СР = ВС*2/3; и, соответственно, площадь треугольника АСР
Sacp = S*2/3; (S - площадь треугольника АВС).
Поскольку площадь треугольника ВАМ равна половине площади АВС, а площадь АКМ равна половине АВМ, то
Sakm = S/4;
Таким образом, площадь четырехугольника КРСМ равна
Skpcm = Sacp - Sakm = S*(2/3 - 1/4) = S*5/12;
ответ 12/5
S=1/2 *ab ;
24=1/2 *ab ;
a=24*2/b=48/b
P=a+b+c ;
24=a+b+c ;
24=48/b+b+c;
c=24-48/b-b
c^2=a^2+b^2
(24-48/b-b)^2=(48/b)^2+b^2
b=6 см a=8 см
или b=8 см a=6 см
тогда с= 10 см
гипотенуза равна диагонали
радиус равен с/2= 10/2=5 см
ответ 5 см