Дано:
∠A=∠A1
AB=A1B1
AC=A1C1
Доказать:
ΔABC=ΔA1B1C1
Доказательство:
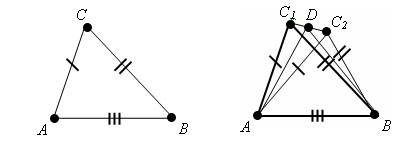
Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны. как то такв середине треугольник не нужен
AB, AC і MN - дотичні, проведені до кола (B, C, K - точки дотику). Знайдіть периметр ΔAMN , якщо AB = 8 см.
Известная теорема: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
MK = MB
NK = NC
AC = AB
P (ΔAMN) =AM + MN + AN = AM +( MK + NK ) +AN =
AM +( MB + NC ) +AN = (AM + MB) + (AN + NC) = AB +AC = 2*AB
ответ: P (ΔAMN) = 2*AB = 2*8 cм = 16 см
•Если прямые не пересекаются, то они параллельны, следовательно, прямая тоже одна (та же самая, что и в первом случае).
•Короче, прямую можно провести только одну.