Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
d = |D2 - D1|
√(A² + B² + C²) .
Для этого уравнение второй плоскости надо привести к одинаковым коэффициентам с первой плоскостью.
5x-3y+z+3=0 и 5x-3y+z+3,5=0
d = |3-3.5|/√(25+9+1) = 0.5/√35 ≈ 0,08452.
Одинаковые расстояния от плоскостей 5x-3y+z+3=0 и 5x-3y+z+3,5=0 равны половине найденной величины. Тогда коэффициент D в уравнении срединной плоскости равен:
D = D1 + (0,08452/2)*√35 = 3 + 0,25 = 3,25.
ответ: 5x-3y+z+3,25=0.
Можно было просто найти среднее значении между D1 и D2 = (3+3,5)/2 = 3,25.
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
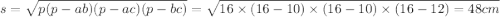
С другой стороны можно S=p×r
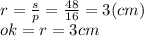
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.