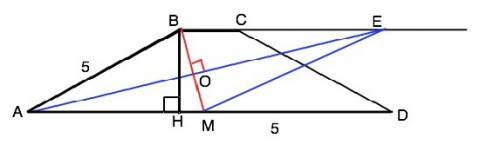
Опустим из вершины В высоту трапеции ВН. Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности, а больший - полусумме оснований. АН=(10-2):2=4 см Из треугольника АВН по т. Пифагора ВН=3 см.
Противоположные стороны трапеции параллельны. Биссектриса угла ВАD при них – секущая. ∠ВЕА=∠ЕАD – накрестлежащие. Но ∠ВАЕ=∠ЕАD, т.к. АЕ - биссектриса. ⇒ ∆ АВЕ - равнобедренный (т.к.углы при основании АЕ равны). АВ=ВЕ=5 см.
Проведем из Е параллельно АВ прямую до пересечения с АD в точке М. В параллелограмме АВЕМ противоположные стороны параллельны и равны, значит, ЕМ=АВ=ВЕ=АМ=5, ⇒ АВЕМ - ромб.
Высота трапеции ВН - высота ромба. Площадь ромба равна произведению высоты на сторону, к которой проведена. Ѕ(АВЕМ)=ВН•АМ=3•5=15 см²
Биссектриса угла АВЕ – меньшая диагональ ромба ВМ и образует с высотой ромба и частью его стороны прямоугольный треугольник ВНМ, в котором ВН и МН - катеты. ВН=3 см, МН=АМ-АН=1см По т.Пифагора ВМ=√(BH²+HM²)=√(9+1)=√10. Биссектриса ВО угла АВЕ в ∆ АВЕ равна половине ВМ. ВО=(√10)/2; BO²=10/4=2,5 см²
V = 1/3 Sосн·Н
Sпп = Sосн + Sбок
Найдем отношение объема пирамиды к площади ее поверхности:
V/Sпп = 1/3 Sосн·Н / Sосн+Sбок
В основании – шестиугольник. Площадь правильного шестиугольника:
S = pr, где р – полупериметр.
Площади боковой поверхности правильной пирамиды:
Sбок = рL/2, где р – периметр, L – апофема.
R = rH / r+L
V/Sпп = 1/3 Sосн·Н / Sосн+Sбок = 1/3 · prH / pr+рL = 1/3 · rH / r+L = 1/3 R
Найдем радиус вписанного шара через объем пирамиды и ее полную поверхность:
R = 3V/Sпп = 3 · 4800 / 2000 = 7,2
ответ: 7,2 (ед.измер.)
и рассмотрим треугольник АВF: он прямоугольный, т.к. АF высота, угол А = 30°, а по определению "катет, лежащий напротив угла 30° равен половине гипотенузы". Гипотенуза у нас см
АF = см.
Длина окружности L = где D диаметр окружности
По определению "Радиус вписанной окружности в трапецию равен половине высоты трапеции." => так как два радиуса - это диаметр, то высота трапеции = диаметру вписанной окружности.
см