0А=6см
Перпендикуляр и наклонные к
плосксти.
Объяснение:
Дано:
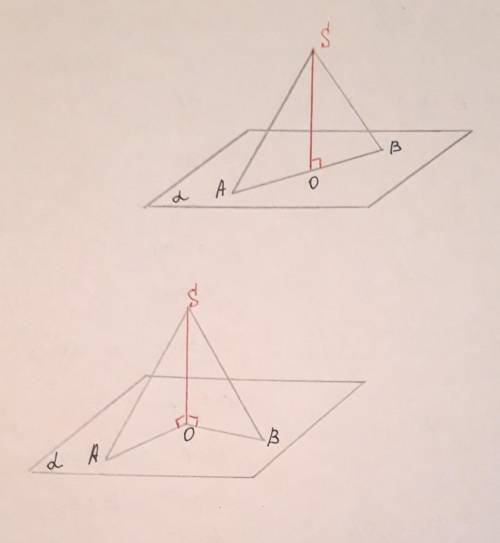
SA, SB - наклонные к
плоскости а
SO - перпендикуляр к а
SB=17см
ОВ=15см
SA=10см
------------------------------------
ОА - ?
SO - перпендикуляр к плос
кости а ==> SO перпендику
лярна прямым ОВ иОА.
Возможны 2 варианта:
1) точки SAОB лежат в одной
плоскости;
2) точки SAОB не лежат в од
ной плоскости.
Решение и ответ одинаковы
для обоих вариантов.
Рассмотрим треугольник SOB:
<SOB=90°
Треуг. SOB - прямоугольный.
По теореме Пифагора:
SO^2=SB^2-OB^2
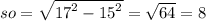
Рассмотрим треугольник SOA:
<SOB=90°
Треуг. SOA - прямоугольный.
По теореие Пифагора:
OA^2=SA^2-SO^2
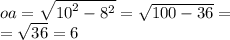
Oтвет:
ОА=6см

Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Уравнение окружности имеет вид:
(х-х0)^2+(y-y0)^2=r2,где (х0;у0) - центр окружности, а r2 - радиус окружности.
Если центр окружности является началом координат, то уравнение принимает такой вид:
х^2+y^2=r^2
Уравнение прямой, проходящей через две точки, имеет вид:
ax+by+c=0
У тебя есть рисунок, чертеж этой прямой. Есть координаты этих двух точек.Необходимо составить два уравнения для каждой из точек. К примеру, есть точка А (-3;2) и В (1;-1).
Для А: -3а+2b+с=0
Для В: a-b+c=0
Эти уравнения возьмем в систему, решим их каким-либо дважды: чтобы исчезла а и чтобы исчезлa b.
У нас получится b=4c; a=3c
Подставим это в наше уравнение:
3сх+4су+с=0
Сократим на с:
3х+4у+1=0
Это и будет уравнением прямой.