Дано:
a = 8см - сторона основания
α = 45° - угол наклона бокового ребра к плоскости основания
A - ? - апофема
Высота h треугольника, лежащего в основании пирамиды
h = a·cos30° = 8·0.5√3 = 4√3
Точка О основания пирамиды, в которую проецируется вершина пирамиды находится на расстоянии 2h/3 от вершины треугольника, лежащего в основании и на h/3 от основания апофемы. Эти расстояния равны соответственно
2h/3 = (8√3)/3 cм и h/3 = (4√3)/3 см.
Поскольку боковое ребро наклонено к плоскости основания под углом α=45°, то высота пирамиды Н = 2h/3 = (8√3)/3 см.
Апофему А тогда найдём по теореме Пифагора
А =√(Н² + (h/3)²) = √(64/3 + 16/3) = √(80/3) = (4√15)/3 ≈ 5,16(см)
ответ: А = (4√15)/3 ≈ 5,16(см)
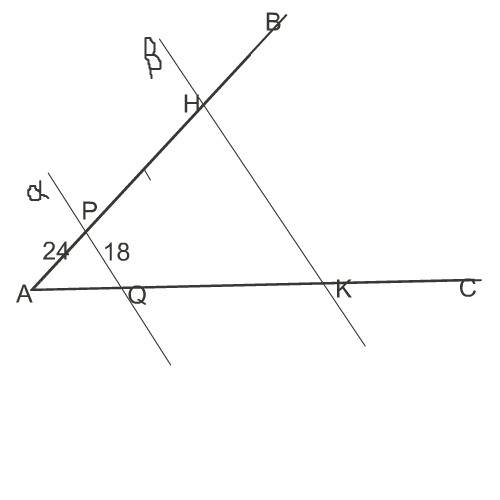
Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках Р и Н, а сторону АС этого угла - соотвптственно в точках Q и К
Найдите:
а) АН и АК если РН= 2РА, РН = 12 см, AQ = 5 см
Задача на подобие треугольников.
Рассмотрим рисунок.
Стороны угла АВС и параллельные плоскости ( на рисунке они изображены прямыми α и β ) образуют пересечением два подобных треугольника,
так как их углы при параллельных основаниях равны по свойству параллельных прямых и секущей.
В треугольнике АНК дано, что отрезок РН = 2 РА.
РН=12, ⇒
РА=12:2=6 см
АН =12+6=18 см
Сторона АН ᐃ АВС пропорциональна стороне АР ᐃ APQ
k=18:6=3
Так как рассматриваемые треугольники подобны, то
АК:АQ=3
АQ=5, ⇒
АК=5·3=15см
б) НК и АН, если PQ = 18 см, АР = 24 см, АН = 3/2 РН
АН = 3/2 РН ⇒
РН=2/3 АН
АР=1/3 АН =24 см
АН=24·3=72 см
Так как k=3,
PQ=1/3 НК ⇒
НК=18·3=54 см
Последовательно вычитаем из 180 21 и ли 49 и находим больший угол.
2) В правильном многоугольнике углы и стороны равны. В правильном многоугольнике, вписанном в окружность углы лежат на окружности, следовательно отрезки соединяющие углы с центром окружности будут радиусы. Все проведенные радиусы к углам правильного многоугольника, деля его на равнобедренные треугольники, одновременно деля углы пополам. Следовательно углы при основании этих треугольников будут равны 70 гр. Следовательно углы при вершине этих треугольников будут равны 180-70-70=40 гр. Их общая сумма равна 360 гр. Отсюда 360:40=9 сторон.