Расстояние от точки до прямой измеряется длиной перпендикуляра. Радиус, проведенный в точку касания, перпендикулярен касательной. Расстояние от центра окружности до касательной равно радиусу.
Если между двумя параллельными прямыми вписана окружность, то расстояние между прямыми равно двум расстояниям от центра до касательной, то есть двум радиусам или диаметру.
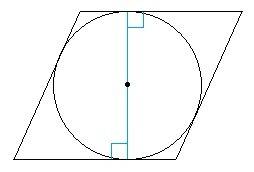
Противоположные стороны ромба параллельны. Расстояние между противоположными сторонами ромба является его высотой и равно двум радиусам вписанной окружности.
Исходя из этого легко увидеть, что доказать это тождество не возможно (возможно только в частном случае: правильный или равнобедренный треугольник).
В левой части равенства расположены касательные, принадлежащие вершинам А и С, а в правой, принадлежащие А и В.
Если АС1=АВ1, то СА1≠А1В.
Доказано, что равенство неверно.