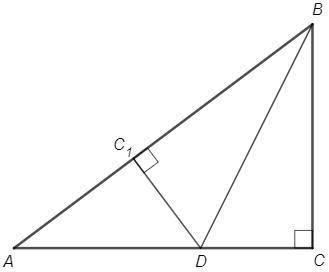
Каждая точка биссектрисы равноудалена от сторон угла, DC=DC1
Площади треугольников с равными высотами относятся как основания.
Треугольники ABD и DBC имеют общую высоту из вершины B и равные высоты из вершины D.
SABD/SDBC =AD/DC =AB/BC
Доказали теорему о биссектрисе в случае прямоугольного треугольника.
Биссектриса делит сторону треугольника в отношении прилежащих сторон.
AD/DC =AB/BC =20/12 =5/3
DC =3/8 AC =6
DBC, т Пифагора
BD =√(BC^2 +DC^2) =6√5 (см)
Или
cosB =BC/AB =3/5
cos(B/2) =√((1+cosB)/2) =√(4/5) =2/√5 (B/2 <90)
BD =BC/cos(B/2) =6√5 (см)
Відповідь: V = 126,75 куб. од.
Пояснення:
У пар - педі AD : AB = 3 : 2 ; S діаг = S кв = 42,25 . V - ?
BD * DD₁ = 42,25 ; BD = DD₁ = c , тоді с² = 42,25 ; с = √42,25 = 6,5.
Нехай AD = 3x , a AB = 2x , тоді із прямок. ΔABD за Т. Піфагора
( 3x )² + ( 2x )² = 6,5² ;
13x² = 42,25 ;
x² = 42,25 : 13 ;
x² = 3,25 ;
x = +√3,25 = 5√0,13 ; AD = 3x = 15√0,13 ; AB = 2x = 10√0,13 .
V = AD * AB * DD₁ ; V = 15√0,13 * 10√0,13 * 6,5 = 150 * 6,5 * 0,13 =
= 126,75 ( куб. од. ) ; V = 126,75 куб. од.