Дано: ромб АВСД
диагональ АС=8,
диагональ ВД=10
Найти: Р=?
S=?
S ромба=0,5(АС*ВД)=0,5(8*10)=0,5*80=40 см²
но АC^2+ВД^2=4АВ^2 тогда 8^2+10^2=4AB^2
64+100=4АВ^2 AB^2=164/4=41
AB=²√ 41=6,403
Р ромба=4*6,403=25,612 см
ответ: Р=25,6см
S=40см²
9 м.
Объяснение:
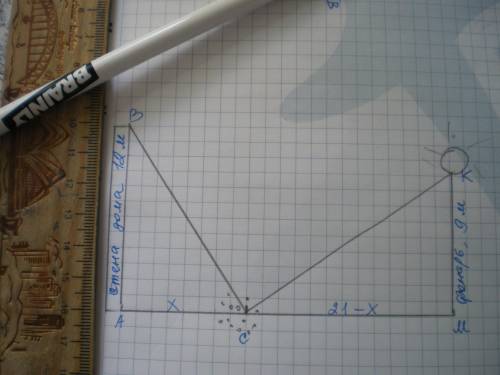
Расстояние от крыши дома до зёрен и от фонаря до зерен представляет собой гипотенузы прямоугольных треугольников АВС и КМС, как показано на рисунке. Если голуби при одинаковой скорости подлетели к корму одновременно, значит, эти гипотенузы равны, ВС=СК.
АВ - стена дома, МК - фонарь. АВ=12 м, МК=9 м.
Пусть искомое расстояние от дома до зерен АС=х м, тогда расстояние от основания столба до зерен СМ=21-х м.
По теореме Пифагора имеем равенство
ВС²=12²+х², а СК²=9²+(21-х)²
Поскольку ВС=СК, равенство принимает вид
12²+х²=9²+(21-х)²
144+х²=81+441-42х+х²
42х=378
х=9.
Расстояние от дома до зёрен 9 м.
ответ: 5 (метров)
Объяснение: Обозначим высоту дома АВ, высоту фонаря МЕ, расстояние между домом и фонарем АМ ( см. рисунок), место, где лежат зерна, обозначим С.
Т.к. и дом, и фонарь перпендикулярны земле, соединив точки В и Е с точкой С, получим прямоугольные треугольники АВС и СЕМ, гипотенузы которых равны (так как голуби летели с равными скоростями и прилетели одновременно к зерну).⇒ ВС=СЕ
Примем АС=х, тогда СМ=17-х.
ВС²=ВА²+АС²
ЕС²=СМ²+ЕМ²
ВА²+АС²=СМ²+ЕМ²
12²+х²=(17-х)²+5², ⇒ 34х=170, х=5 (метров) = расстояние от дома до зерна.

площадь равна половине произведения диагоналей, (8*10)/2=40
периметр ромба равен 4а
а- сторона ромба
через прямоугольный треугольник находим сторону ромба по теореме пифагора (О- тоска пересечения диагоналей)
BC^2=BO^2+CD^2, где ВО=8/2=4 СО=10/2=5
ВС=6
периметр =24
ответ:площадь=40
периметр=24