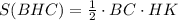, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
.
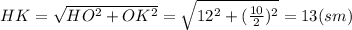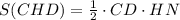, где НN - высота, проведенная к стороне СD.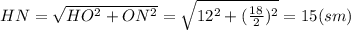
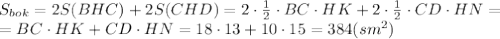
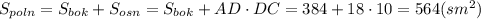
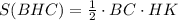, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.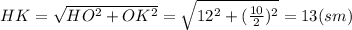.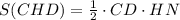, где НN - высота, проведенная к стороне СD.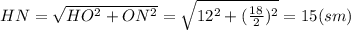
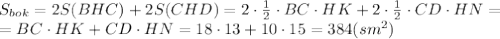
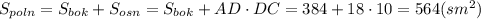
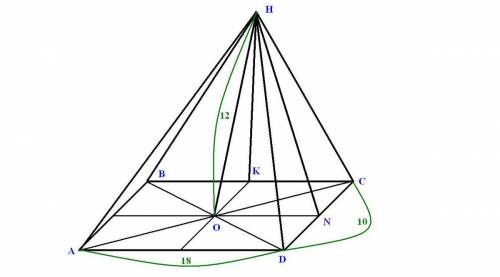
Δ АВД правильный (АВ=АД, ∠А=60°), значит ВД=АВ.
Тр-ки КДА, КДВ и КДС равны (АД=ВД=СД, КД - общая сторона и все прямоугольные). КА=КВ=КС.
В ΔКДА КА²=КД²+АД²=14²+6²=232.
КА=КВ=КС=2√58 см.