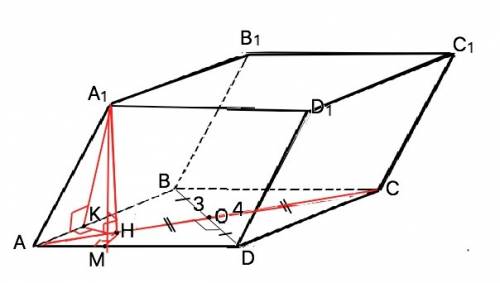
Обозначим вершины параллелепипеда АВСDD1FА1В1С1. Формула объема параллелепипеда V=S•H, где Ѕ - площадь грани, лежащей в основании, Н - высота, т.е. расстояние между параллельными (горизонтальными) гранями.
Ѕ(ромба)=d•d1/2=BD•AC/2=6•8/2=24 см² Диагонали ромба взаимно перпендикулярны и делят его на 4 равных прямоугольных треугольника, катеты которых равны половинам диагоналей. Из соотношения катетов 3:4, эти треугольники – так называемые египетские, ⇒ гипотенузы этих треугольников -стороны ромба– равны 5 см.
По условию все грани параллелепипеда - равные ромбы, ⇒ боковое ребро составляет с соседними сторонами основания равные углы. ∠А1АК=∠А1АМ. Площади равных граней равны, а их высоты – равные перпендикуляры.⇒ А1К=А1М. Из формулы площади параллелограмма h=S:a=24/5 см. По т.Пифагора АК=√(AA1²-A1К²)=√(5²-(24/5)²)=7/5 см.
Треугольники АКА1 и АМА1 равны по катетам и общей гипотенузе АА1 Проекции равных наклонных А1К и А1М равны. ⇒ НК=НМ. Отсюда прямоугольные ∆ АКН=∆ АМН, их острые углы равны. Поэтому основание высоты А1Н параллелепипеда лежит на биссектрисе угла ВАD, т.е. на диагонали ромба. Прямоугольные ∆ АКН ~∆ АВО по общему острому углу при А. Из подобия следует отношение АН:АВ=АК:АО ⇒АН:5=(7/5):4 ⇒ АН=7/4. т.Пифагора А1Н=(√(AA1²-АН*)=√((400-49):4))=√(9•39/16). АН=0,75√39. V(параллелеп)=24• 0,75√39=18√39 или ≈ 112,41 см³
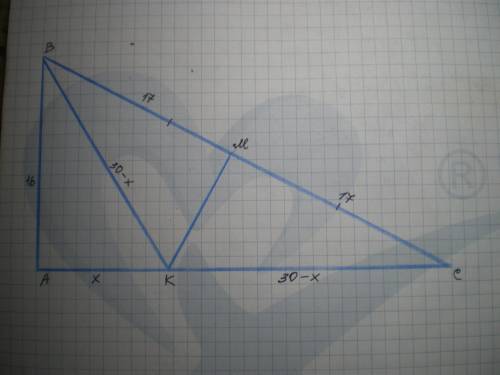
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
По теореме биссектрис АВ/ВС=АМ/СМ=15/9,
Пусть коэффициент отношения равен х, тогда
АВ/ВС=15х/9х.
В тр-ке АВС по теореме Пифагора АВ²=ВС²+АС²,
(15х)²=(9х)²+24²,
225х²=81х²+576,
х=2.
ВС=9х=18 см.
Площадь тр-ка АВС: S=ВС·АС/2=18·9/2=81 см² - это ответ.