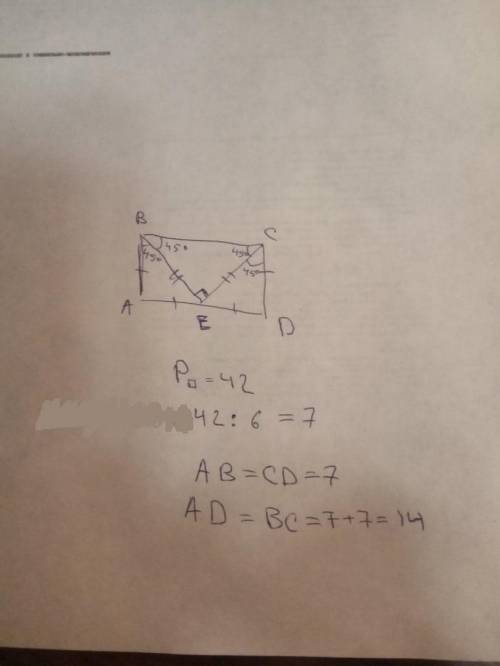
ответ: АВ=CD=7 AD=BC=14
Объяснение: назовем точку снизу как Е. треугольник ВЕС будет равнобедренным и прямоугольным, т.к. точка Е делит сторону АD пополам. Следовательно катеты треугольника будут равны и углы EBC и ECB будут равны 45 градусам. Далее следует что углы АВЕ, ECD, ВЕА и CED будут равны 45 градусам, и отсюда следует, что треугольники ABE и ECD так же равнобедренные и прямоугольные. Отсюда следует, что AB=AE=ED=CD, а сторона ВС = AD и BC = АЕ+ЕD.
Далее делим 42 на 6 = 7 (стороны АВ и CD)
а стороны AD и BC будут равны 7+7 = 14 , так как АЕ=ЕD
АВЕ = 104° Следовательно АВС=76 (смежные углы)
, DСF = 76° следовательно АСВ=76 (вертикальные)
САВ- равнобедренный треугольник
АС = АВ= 12 см.
2.В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый
Значит, DМЕ -тупой (смежные углы) и самый большой в треугольнике ЕМD. Против большего угла лежит большая сторона. Следовательно, DE>DM. Что и требовалось доказать
Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
а-сторона, а+9 - основание треугольника
а+а+а+9=45
3а= 36
Стороны треугольника равны: а=12 а+9=21
12+12+21= 45
ответ: Р = 240 см.
Объяснение:
Рассмотрим 4-угольник ANCM:
Угол NCM = 360 - угол MAN - 90 - 90 (так как AN,AM - высоты) = 360 - 180 - 60 = 120 градусов, причём по свойствам ромба угол NCM равен углу BAD.
Теперь рассмотрим сам ромб. Так как его тупые углы нам известны, то можно найти острые углы:
Угол ADC равен углу ABC и равен (360 - 120 -120)/2 = 120/2 = 60 градусов.
Рассмотрим треугольник ADM. Он прямоугольный с углом AMD = 90 градусов (АМ - высота). Найдём угол DAM:
Угол DAM равен (180 - 90 - угол ADM) = (90 - угол ADC) = (90 - 60) = 30 градусов. Катет против угла в 30 градусов равен половине гипотенузы, то есть DM = 1/2 AD => AD = 2DM = 2 * 30 = 60 см.
Так как в ромбе все стороны равны, то Рромба = 4 * AD = 4 * 60 = 240 см.