Объяснение:
1)
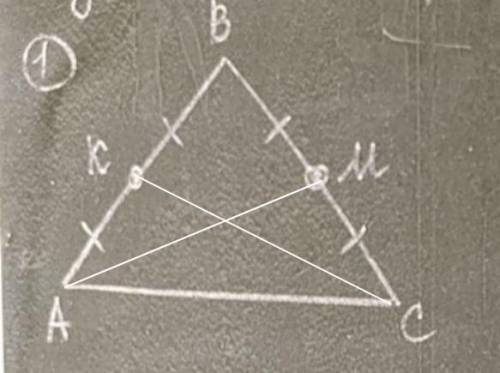
<ВАС=<ВСА, так как ∆АВС- равнобедренный (ВА=ВС, по условию).
КА=МС, по условию.
АС, общая сторона треугольников ∆АКС и ∆МСА.
∆АКС=∆МСА, по первому признаку (две стороны и угол между ними).
Соответственно СК=АМ=9см.
ответ:9см.
2)
<А=<А1, по условию
<С=<С1, по условию
АС=А1С1, по условию.
∆АВС=∆А1В1С1, по второму признаку.
Треугольники равны, то и периметры тоже равны.
РАВС=РА1В1С1.
Пусть сторона АВ будет 2х см, сторона ВС будет 3х см, а сторона АС будет 4х см.
Периметр равен 36. Составляем уравнение.
2х+3х+4х=36
9х=36
х=36/9
х=4
Сторона АВ=2х, подставляем значение х.
2*4=8см.
ответ: АВ=8см.
(Рисунок во вложении)
Отрезки АВ и А1В1 касаются своими концами А, А1 и В, В1 плоскостей бета и альфа соответственно. Проведем перпендикуляры с пунктов В и В1, они пересекают плоскость бета в пунктах С и С1. АС и А1С1 проекции отрезков АВ и А1В1 на плоскость бета. У нас есть 2 прямоугольных треугольника АВС и А1В1С1. Раз отношение их катетов АС и А1С1 = 5:9, то мы можем обозначить АС через 5х, а А1С1 через 9х. ВС = В1С1 обозначим их через у (расстояния между двумя параллельными плоскостями) найдем их по теореме Пифагора из треугольников АВС и А1В1С1. (во вложении).
у = ВС = В1С1=24 (это и есть наше расстояние)
Угол АОС равен углу ДОВ, так как они вертикальные.
АО = ОВ (так как О - середина АВ)
ОС=ОД (так как О - середина СД), ⇒
Треугольники равны по двум сторонам и углу между ними, откуда следует равенство сторон АС и ВД.
2) Рассмотрим треугольники СОВ и АОД.
Угол СОД равен углу АОД, так как они вертикальные.
СО = ОД (по доказанному)
ОВ = ОД (по доказанному), ⇒
Треугольники равны по двум сторонам и углу между ними, откуда следует равенство сторон СВ и АД.
3) Рассмотрим треугольники АСВ и ВДА.
АВ - общая сторона.
АС = ВД (по доказанному)
ВС = АД (по доказанному), ⇒
Треугольники равны по трём сторонам (третий признак равенства треугольников), что и требовалось доказать.